Question

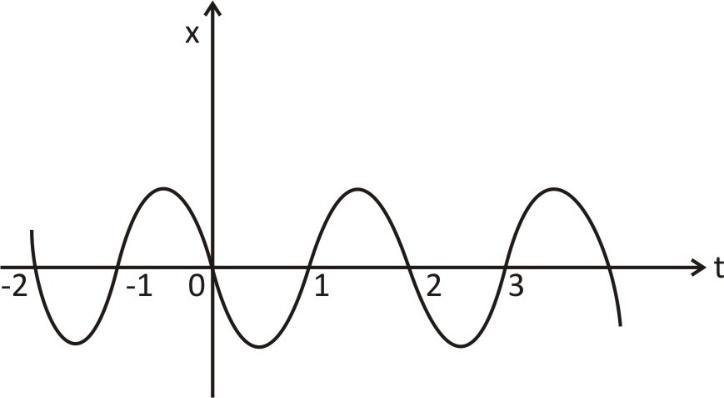
Figure gives the x-plot of a particle executing one-dimensional simple harmonic motion. Give the signs of position, velocity and acceleration variables of the particles at $t = 0.3\,s$ , $1.2\,s$ and $- 1.2\,s$ .

Answer 1

Here we have to use the concepts of simple harmonic motion.
Simple harmonic motion can be defined as an oscillatory motion in which the acceleration of the particle at any point is directly proportional to the displacement of the mean position.

Complete step by step answer:
Maximum acceleration in simple harmonic motion is given by:
${a_{\max }} = {\omega ^2}x$

Where ${a_{\max }}$ is the maximum acceleration, $\omega$ is the angular frequency and $x$ is the displacement.
Maximum velocity in simple harmonic motion is given by:
${v_{\max }} = \omega x$

Where ${v_{\max }}$ is the maximum velocity, $\omega$ is the angular frequency and $x$ is the displacement.
When
$t = 0.3\,s$

Where $t$ is the time-period in the graph.
There's a negative $x$ . The $x - t$ plot gradient is negative as well. Both position and velocity, thus, are negative. However, the acceleration of the particle will be positive, using equation (i).
When
$t = 1.2\,s$

There's a positive $x$ . The $x - t$ plot gradient is positive as well. Both position and velocity, thus, are positive. However, the acceleration of the particle will be negative, using equation (i).
When
$t = - 1.2\,s$

$x$ is negative in this time period. The $x - t$ plot slope is positive. The velocity, then, becomes positive. It can be concluded from equation (i) that the particle's acceleration would be positive.

Additional Information:
- Not all oscillatory motions are simple harmonic in nature whereas all harmonic motions are periodic and oscillatory. Oscillatory motion is often referred to as the harmonic motion of all oscillatory movements, the most important of which is basic harmonic motion.
- In oscillatory motion displacement, velocity and acceleration and force differ in a manner that can be represented by either sine or cosine functions usually referred to as sinusoids.
- In a simple harmonic motion the return of force or acceleration acting on the particle should always be equal to the displacement of the particle and be oriented towards the equilibrium state.
- The amplitude is actually the maximum displacement of the object from the direction of equilibrium. In other words, the same equation refers to the position of an object experiencing basic harmonic motion and to one component of the position of an object experiencing uniform circular motion.
- In basic harmonic motion, the speed and displacement of the target is zero at an extreme location.

Note:
Here we have to carefully observe the time interval of the graph. If we make mistakes in the time intervals then the answers would be wrong. Also we have to know how the velocity-time graph works.
Velocity-Time Graph of uniform acceleration of an object- t he slope of the curve is a continuous line while the time graph of velocity is plotted with an object travelling with uniform acceleration. The graph's slope pattern reveals that the target is travelling with uniform acceleration.