Question
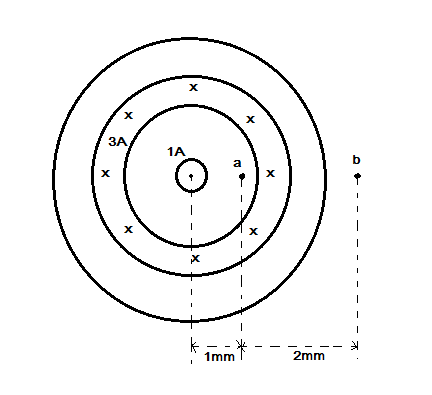
Question: Figure given in the question is a cross sectional view of a coaxial cable. The centre conductor is s...
Figure given in the question is a cross sectional view of a coaxial cable. The centre conductor is surrounded by a rubber layer, which is surrounded by an outer conductor, which is surrounded by another rubber layer. The current in the inner conductor is 1A , out of the page and the current in the outer conductor is 3A into the page. Determine the magnitude and direction of the magnetic field at points a and b.
Solution
Hint : The magnetic field inside a hollow current carrying conductor is zero. Then by using the formula for magnitude of magnetic field at a point due to straight current carrying conductor find the magnetic field due to both the conductors at the given points. Use the right hand thumb rule to find the direction of the magnetic fields.
B=2πdμ0i , where B is the magnetic field at point due to a straight current carrying conductor of i that is at perpendicular distance d. μ0 is permeability of free space and μ0=4π×10−7TmA−1 .
Complete Step By Step Answer:
Let us first find the magnitude and direction of the magnetic field at point a.
Here, since the point a is inside the conductor that is carrying current of 3 A, the magnetic field due to this conductor at point a is zero.
The perpendicular distance between point a and the inner conductor (carrying current of 1 A) is d1=1mm=10−3m .
Therefore, the magnitude of the magnetic field at point a due to the inner conductor is equal to B=2πd1μ0i1
⇒B=2π×10−34π×10−7×1=2×10−4T
This means that the magnitude of the magnetic field at point a is 2×10−4T .
By the right hand thumb rule we get that direction of the magnetic field is upwards.
Now let us find the magnetic field at point b.
The perpendicular distance between point b and the axis of the two conductors is d=3mm=3×10−3m .
Therefore, the magnetic field at point b due to outer conductor is B2=2πdμ0i2=2π×3×10−34π×10−7×3=2×10−4T
By the right hand thumb rule, the direction of this magnetic field is downwards.
Now, the magnetic field at point b due to inner conductor is B1=2πdμ0i1=2π×3×10−34π×10−7×1=32×10−4T .
And the direction of this magnetic field is upwards.
Since the two magnetic fields are opposite in directions, the magnitude of the net magnetic field is B=B2−B1 in the downward direction.
Then,
⇒B=2×10−4−32×10−4=34×10−4T
The magnetic field at point b is 34×10−4T in the downward direction.
Note :
If you do not know that the magnitude of magnetic field inside a hollow conductor is equal to zero, then you can use the Ampere’s law. According to Ampere’s law, the integral of magnetic field and the circumference of a closed loop is equal to μ0 times the net current passing inside the loop.
If the magnetic field is constant then the ampere’s law is given as Bl=μ0iin , where l is the circumference of the loop and iin is the net current passing through the loop.
