Question
Question: Figure given in the question is a cross sectional view of a coaxial cable. The centre conductor is s...
Figure given in the question is a cross sectional view of a coaxial cable. The centre conductor is surrounded by a rubber layer, which is surrounded by an outer conductor, which is surrounded by another rubber layer. The current in the inner conductor is 1.0 A out of the page, and the current in the outer conductor is 3.0 A into the page. Determine the magnitude and direction of the magnetic of the magnetic field at points a and b.
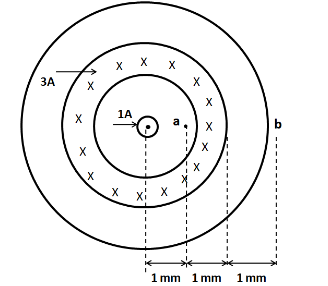
Solution
Hint : To solve this question, we need to use the Ampere’s circuital law. As the current distribution is symmetric, so this method would be the most convenient.
Formula used: ∮B∙dl=μ0I
where B is the magnetic field, I is the current flowing through the conductor, and μ0 is the permittivity of free space.
Complete step by step answer
We know that the Ampere’s circuital law is given by
∮B∙dl=μ0I ………………..(1)
So, we need to find the current enclosed within the surface enclosed by the boundary around the points.
For point a:
At the point a, we draw an imaginary circle of radius ra=1mm as shown in the below diagram.
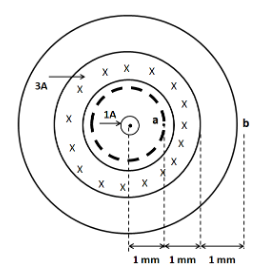
As we can see in the diagram, the current enclosed inside the region of this circle is
I=1A (Outwards ∙ )
From equation (1)
∮Ba∙dl=μ0(1)
As the current distribution is symmetrical around the region, so the magnetic field Ba is constant around the circle. So, it can be taken out of the integral.
Thus, we have
Ba∮dl=μ0(1)
Ba(2πra)=μ0
As ra=1mm=10−3m , we have
Ba(2π×10−3)=μ0
Ba=2πμ0×103
We know that μ0=4π×10−7
Ba=2π4π×10−7×103
Ba=2×10−4T
Hence, the magnetic field at point a is 2×10−4T
As the net current enclosed is in the outward direction, so by the right hand thumb rule, this magnetic field is in an anti-clockwise direction.
For point b:
At point b, we draw an imaginary circle of radius rb=3mm as shown in the below diagram.
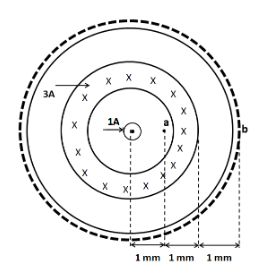
As we can see in the diagram, the current enclosed inside the region of this circle is 3A ⊗ and 1A ∙
So, net current enclosed is
I=3A−1A (Inwards ⊗ )
I=2A
From equation (1)
∮Bb∙dl=μ0(2)
As the current distribution is symmetrical around the region, so the magnetic field Bb is constant around the circle. So, it can be taken out of the integral.
Thus, we have
Bb∮dl=μ0(2)
Bb(2πrb)=2μ0
As rb=3mm=3×10−3m , we have
Bb(2π×3×10−3)=2μ0
Ba=6π2μ0×103
We know that μ0=4π×10−7
Ba=6π2×4π×10−7×103
Ba=1.33×10−4T
Hence, the magnetic field at point b is 1.33×10−4T
As the net current enclosed is in the inward direction, so by the right hand thumb rule, this magnetic field is in clockwise direction.
Note
The ampere’s circuital law is very much convenient in the case of symmetric current distributions. This is because in these cases the magnetic field becomes constant over the loop of the integration and hence the integration becomes simple. But in the cases of non-symmetric current distributions, the integration may become complex and this method may not be useful.
