Question
Question: $\frac{1}{v}-\frac{1}{u}=\frac{1}{f}$, ...
v1−u1=f1,
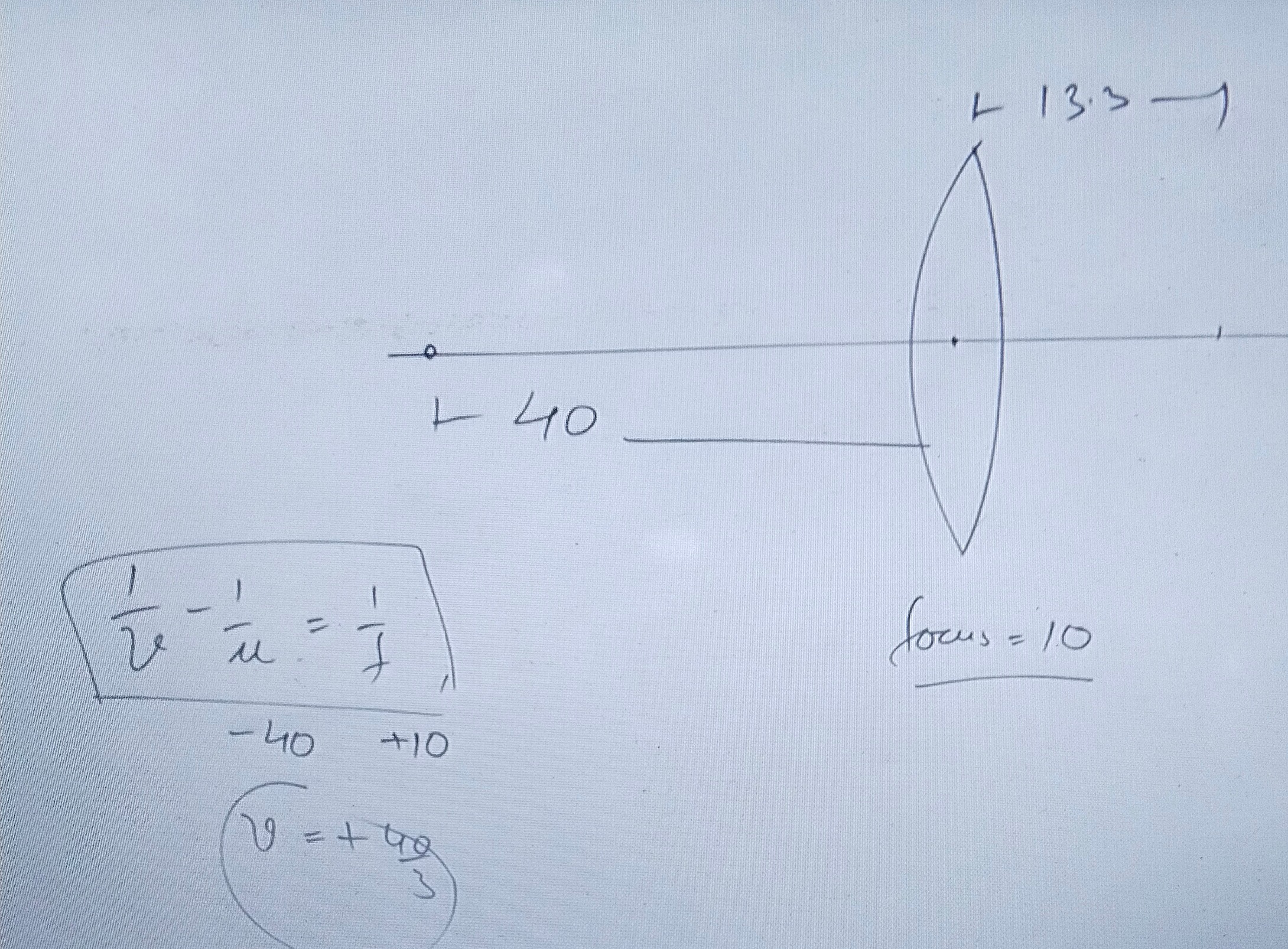
Answer
v = 40/3
Explanation
Solution
We are given the lens equation
v1−u1=f1with the values
u=−40,f=+10.Substitute the values into the equation:
v1−−401=101⟹v1+401=101.Rearrange to solve for v1:
v1=101−401=404−1=403.Taking the reciprocal gives:
v=340.Minimal Explanation: Substitute u=−40 and f=10 in v1−u1=f1 to get v1=101−(−401)=403 so v=340.
