Question
Question: Find $I=?$...
Find I=?
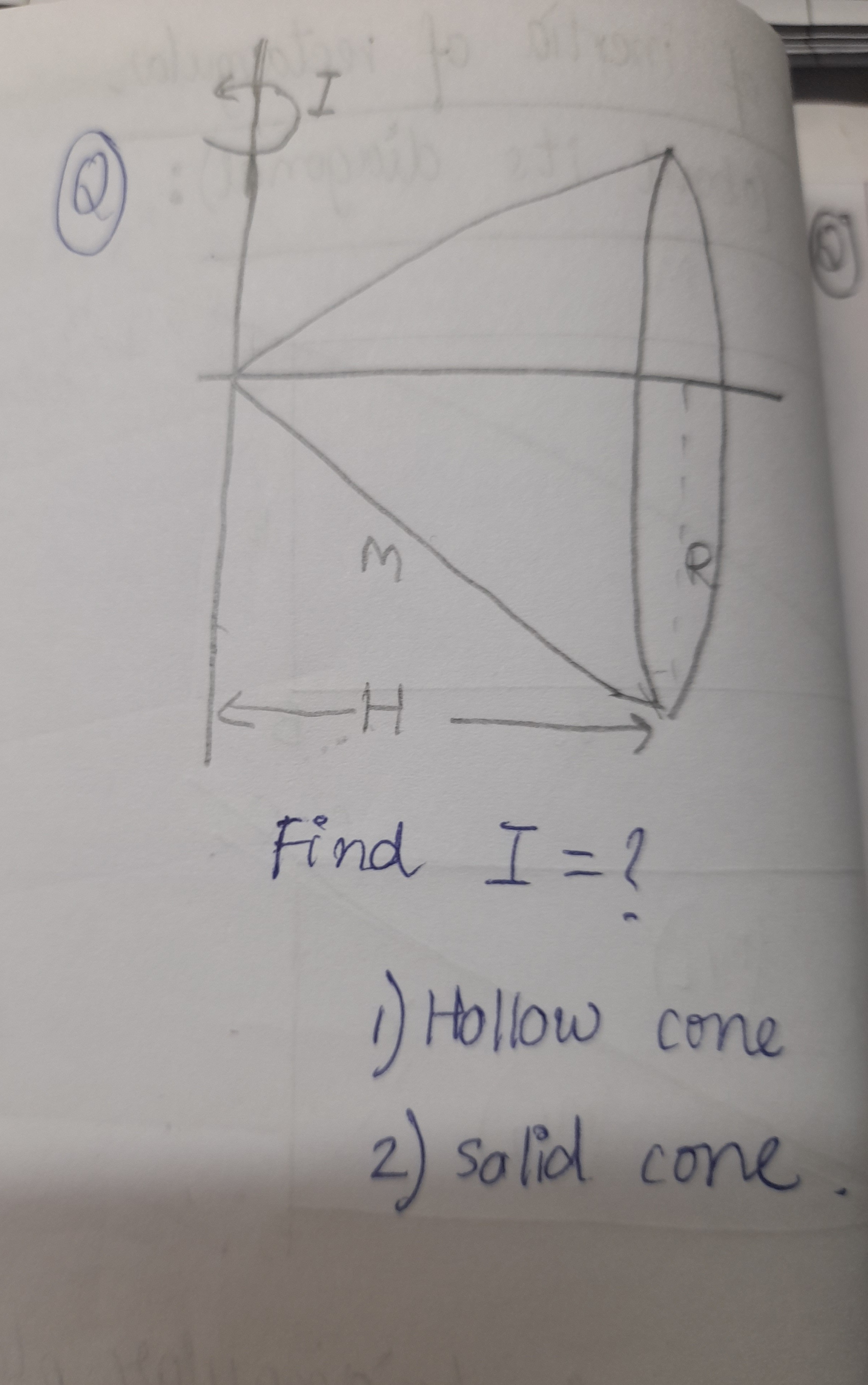
- I=21MR2, 2) I=103MR2
Solution
The problem asks to find the moment of inertia (I) for a hollow cone and a solid cone, both of mass M, height H, and base radius R, about their central axis.
1. Hollow Cone
A hollow cone can be considered as a collection of infinitesimally thin rings. Let's consider an elemental ring at a distance x from the apex along the height. The radius of this elemental ring is r, and its width along the slant height is dl.
From similar triangles (referring to the cone's cross-section): The ratio of radius to height is constant: xr=HR⟹r=HRx.
Let L be the slant height of the cone, L=R2+H2. The slant height l to the elemental ring is related by xl=HL⟹l=HLx. The elemental width along the slant height is dl=HLdx.
The total surface area of the hollow cone is A=πRL. The surface mass density σ=AM=πRLM.
The area of the elemental ring is dA=(2πr)dl. Substituting r and dl: dA=2π(HRx)(HLdx)=H22πRLxdx.
The mass of the elemental ring is dm=σdA. dm=πRLM⋅H22πRLxdx=H22Mxdx.
The moment of inertia of a thin ring of mass dm and radius r about its central axis is dI=dm⋅r2. dI=(H22Mxdx)(HRx)2=H22Mxdx⋅H2R2x2=H42MR2x3dx.
To find the total moment of inertia, integrate dI from x=0 to x=H: I=∫0HH42MR2x3dx=H42MR2∫0Hx3dx I=H42MR2[4x4]0H=H42MR2(4H4−0) I=42MR2=21MR2.
2. Solid Cone
A solid cone can be considered as a stack of infinitesimally thin disks. Let's consider an elemental disk at a distance x from the apex along the height. The radius of this elemental disk is r, and its thickness is dx.
From similar triangles: xr=HR⟹r=HRx.
The total volume of the solid cone is V=31πR2H. The volume mass density ρ=VM=31πR2HM=πR2H3M.
The volume of the elemental disk is dV=πr2dx. Substituting r: dV=π(HRx)2dx=H2πR2x2dx.
The mass of the elemental disk is dm=ρdV. dm=πR2H3M⋅H2πR2x2dx=H33Mx2dx.
The moment of inertia of a thin disk of mass dm and radius r about its central axis is dI=21dm⋅r2. dI=21(H33Mx2dx)(HRx)2=21H33Mx2dx⋅H2R2x2=2H53MR2x4dx.
To find the total moment of inertia, integrate dI from x=0 to x=H: I=∫0H2H53MR2x4dx=2H53MR2∫0Hx4dx I=2H53MR2[5x5]0H=2H53MR2(5H5−0) I=103MR2.
The moments of inertia are:
- Hollow cone: I=21MR2
- Solid cone: I=103MR2
