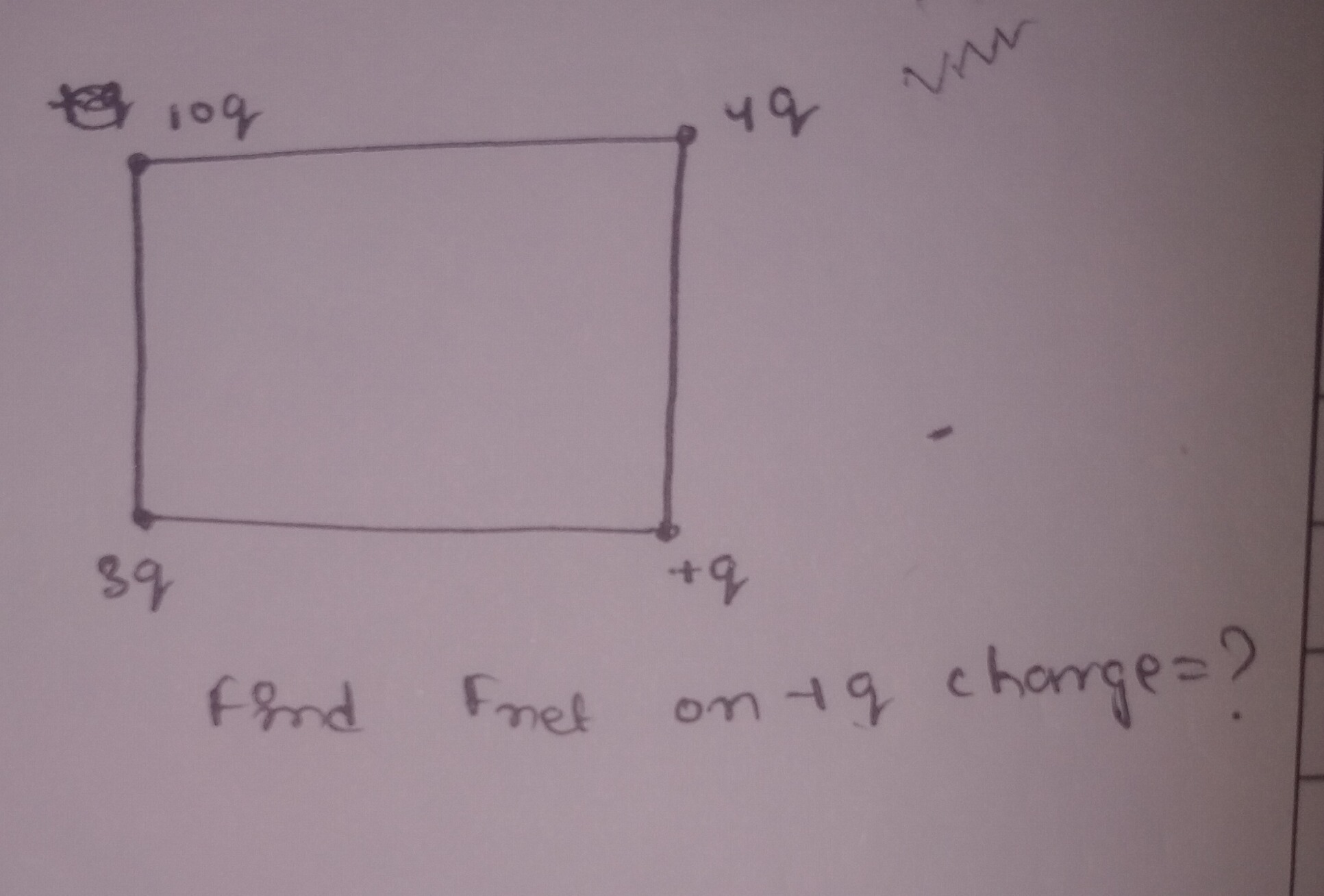
Question

Find $F_{net}$ on +q charge=?

Answer 1

$\frac{kq^2}{a^2} \sqrt{50 + 35\sqrt{2}}$

Answer 2

Let the side length of the square be 'a'.

Let the charge on which the net force is to be found be $Q = +q$. This charge is located at the bottom-right corner.

The other charges are:

1. $Q_1 = 10q$ at the top-left corner.
2. $Q_2 = 4q$ at the top-right corner.
3. $Q_3 = 3q$ at the bottom-left corner.

All charges are positive, so all forces will be repulsive. Let's define a coordinate system where the charge $Q=+q$ is at the origin $(0,0)$. Then the positions of the other charges are:

• $Q_3 = 3q$ at $(-a, 0)$
• $Q_2 = 4q$ at $(0, a)$
• $Q_1 = 10q$ at $(-a, a)$

Let $k = \frac{1}{4\pi\epsilon_0}$.

1. Force due to $Q_3 = 3q$ on $Q=+q$ ($F_3$):

• Distance $r_3 = a$.
• The force is repulsive, acting along the positive x-axis (from $Q_3$ to $Q$).
• Magnitude: $F_3 = k \frac{Q_3 Q}{r_3^2} = k \frac{(3q)(q)}{a^2} = \frac{3kq^2}{a^2}$
• Vector form: $\vec{F}_3 = \frac{3kq^2}{a^2} \hat{i}$

2. Force due to $Q_2 = 4q$ on $Q=+q$ ($F_2$):

• Distance $r_2 = a$.
• The force is repulsive, acting along the negative y-axis (from $Q_2$ to $Q$).
• Magnitude: $F_2 = k \frac{Q_2 Q}{r_2^2} = k \frac{(4q)(q)}{a^2} = \frac{4kq^2}{a^2}$
• Vector form: $\vec{F}_2 = -\frac{4kq^2}{a^2} \hat{j}$

3. Force due to $Q_1 = 10q$ on $Q=+q$ ($F_1$):

• Distance $r_1 = \sqrt{(-a-0)^2 + (a-0)^2} = \sqrt{a^2 + a^2} = a\sqrt{2}$.
• The force is repulsive, acting along the diagonal from $Q_1$ to $Q$. The direction vector from $Q_1(-a,a)$ to $Q(0,0)$ is $(0 - (-a))\hat{i} + (0-a)\hat{j} = a\hat{i} - a\hat{j}$.
• The unit vector in this direction is $\frac{a\hat{i} - a\hat{j}}{a\sqrt{2}} = \frac{1}{\sqrt{2}}(\hat{i} - \hat{j})$.
• Magnitude: $F_1 = k \frac{Q_1 Q}{r_1^2} = k \frac{(10q)(q)}{(a\sqrt{2})^2} = k \frac{10q^2}{2a^2} = \frac{5kq^2}{a^2}$
• Vector form: $\vec{F}_1 = F_1 \times \frac{1}{\sqrt{2}}(\hat{i} - \hat{j}) = \frac{5kq^2}{a^2 \sqrt{2}} (\hat{i} - \hat{j}) = \frac{5kq^2}{a^2 \sqrt{2}} \hat{i} - \frac{5kq^2}{a^2 \sqrt{2}} \hat{j}$

Net Force ($F_{net}$):

The net force is the vector sum of these three forces: $\vec{F}_{net} = \vec{F}_3 + \vec{F}_2 + \vec{F}_1$

$\vec{F}_{net} = \left(\frac{3kq^2}{a^2} \hat{i}\right) + \left(-\frac{4kq^2}{a^2} \hat{j}\right) + \left(\frac{5kq^2}{a^2 \sqrt{2}} \hat{i} - \frac{5kq^2}{a^2 \sqrt{2}} \hat{j}\right)$

Group the x and y components: $F_x = \frac{3kq^2}{a^2} + \frac{5kq^2}{a^2 \sqrt{2}} = \frac{kq^2}{a^2} \left(3 + \frac{5}{\sqrt{2}}\right)$ $F_y = -\frac{4kq^2}{a^2} - \frac{5kq^2}{a^2 \sqrt{2}} = -\frac{kq^2}{a^2} \left(4 + \frac{5}{\sqrt{2}}\right)$

Let $F_0 = \frac{kq^2}{a^2}$. $F_x = F_0 \left(3 + \frac{5\sqrt{2}}{2}\right) = F_0 \left(\frac{6 + 5\sqrt{2}}{2}\right)$ $F_y = -F_0 \left(4 + \frac{5\sqrt{2}}{2}\right) = -F_0 \left(\frac{8 + 5\sqrt{2}}{2}\right)$

The magnitude of the net force is: $F_{net} = \sqrt{F_x^2 + F_y^2}$ $F_{net} = \sqrt{\left[F_0 \left(\frac{6 + 5\sqrt{2}}{2}\right)\right]^2 + \left[-F_0 \left(\frac{8 + 5\sqrt{2}}{2}\right)\right]^2}$ $F_{net} = \frac{F_0}{2} \sqrt{(6 + 5\sqrt{2})^2 + (8 + 5\sqrt{2})^2}$ $F_{net} = \frac{F_0}{2} \sqrt{(36 + 60\sqrt{2} + 50) + (64 + 80\sqrt{2} + 50)}$ $F_{net} = \frac{F_0}{2} \sqrt{(86 + 60\sqrt{2}) + (114 + 80\sqrt{2})}$ $F_{net} = \frac{F_0}{2} \sqrt{200 + 140\sqrt{2}}$ $F_{net} = F_0 \sqrt{\frac{200 + 140\sqrt{2}}{4}}$ $F_{net} = F_0 \sqrt{50 + 35\sqrt{2}}$

Substituting $F_0 = \frac{kq^2}{a^2}$: $F_{net} = \frac{kq^2}{a^2} \sqrt{50 + 35\sqrt{2}}$

The direction of the net force is given by $\theta = \arctan\left(\frac{F_y}{F_x}\right)$. Since $F_x > 0$ and $F_y < 0$, the net force is in the fourth quadrant.

Explanation of the solution:

1. Identify all charges and their positions relative to the charge of interest (+q).
2. Calculate the electrostatic force exerted by each individual charge on the +q charge using Coulomb's Law ($F = k \frac{Q_1 Q_2}{r^2}$).
3. Determine the direction of each force. Since all charges are positive, all forces are repulsive.
4. Resolve each force into its x and y components.
5. Sum the x-components and y-components separately to find the net x-component ($F_x$) and net y-component ($F_y$) of the force.
6. Calculate the magnitude of the net force using $F_{net} = \sqrt{F_x^2 + F_y^2}$.

Answer:

The net force on the +q charge is $\frac{kq^2}{a^2} \sqrt{50 + 35\sqrt{2}}$, where 'a' is the side length of the square and $k = \frac{1}{4\pi\epsilon_0}$.