Question

Find angular momentum of the rolling body about point P shown in figure, at time t = 2 s in each of the following cases

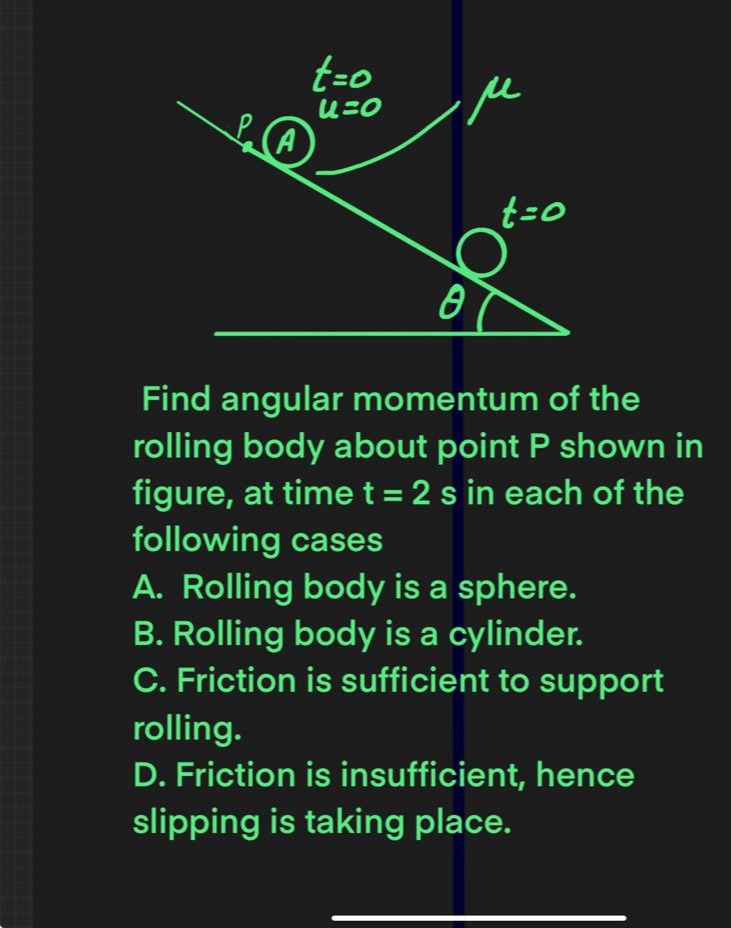
• A. Rolling body is a sphere.
• B. Rolling body is a cylinder.
• C. Friction is sufficient to support rolling.
• D. Friction is insufficient, hence slipping is taking place.

Answer 1

A. Rolling body is a sphere: $L_P(2) = \frac{4}{7}MR g \sin\theta$ B. Rolling body is a cylinder: $L_P(2) = \frac{2}{3}MR g \sin\theta$ C. Friction is sufficient to support rolling: $L_P(2) = \frac{2cMR g \sin\theta}{1+c}$, where $I_{CM} = cMR^2$. D. Friction is insufficient, hence slipping is taking place: $L_P(2) = 2\mu_k MR g \cos\theta$

Answer 2

The angular momentum about point P is given by $\vec{L}_P = \vec{r}_{CM/P} \times M\vec{v}_{CM} + I_{CM}\vec{\omega}$. Since $\vec{r}_{CM/P}$ and $\vec{v}_{CM}$ are collinear, the first term is zero, so $\vec{L}_P = I_{CM}\vec{\omega}$.

For rolling without slipping (Cases A, B, C), the acceleration is $a = \frac{g \sin\theta}{1 + I_{CM}/(MR^2)}$ and angular acceleration is $\alpha = a/R$. The angular velocity at $t=2$ s is $\omega(2) = \alpha \times 2$.

Case A (Sphere): $I_{CM} = \frac{2}{5}MR^2$. $a = \frac{5}{7}g \sin\theta$. $\alpha = \frac{5g \sin\theta}{7R}$. $\omega(2) = \frac{10g \sin\theta}{7R}$. $L_P(2) = \frac{2}{5}MR^2 \times \frac{10g \sin\theta}{7R} = \frac{4}{7}MR g \sin\theta$.

Case B (Cylinder): $I_{CM} = \frac{1}{2}MR^2$. $a = \frac{2}{3}g \sin\theta$. $\alpha = \frac{2g \sin\theta}{3R}$. $\omega(2) = \frac{4g \sin\theta}{3R}$. $L_P(2) = \frac{1}{2}MR^2 \times \frac{4g \sin\theta}{3R} = \frac{2}{3}MR g \sin\theta$.

Case C (Sufficient friction): $I_{CM} = cMR^2$. $a = \frac{g \sin\theta}{1+c}$. $\alpha = \frac{g \sin\theta}{(1+c)R}$. $\omega(2) = \frac{2g \sin\theta}{(1+c)R}$. $L_P(2) = cMR^2 \times \frac{2g \sin\theta}{(1+c)R} = \frac{2cMR g \sin\theta}{1+c}$.

Case D (Insufficient friction): Kinetic friction $f_k = \mu_k N = \mu_k Mg \cos\theta$. Linear acceleration $a = g \sin\theta - f_k/M = g \sin\theta - \mu_k g \cos\theta$. Angular acceleration $\alpha = \frac{f_k R}{I_{CM}} = \frac{\mu_k Mg \cos\theta R}{cMR^2} = \frac{\mu_k g \cos\theta}{cR}$. Angular velocity $\omega(2) = \alpha \times 2 = \frac{2\mu_k g \cos\theta}{cR}$. Angular momentum $L_P(2) = I_{CM}\omega(2) = cMR^2 \times \frac{2\mu_k g \cos\theta}{cR} = 2\mu_k MR g \cos\theta$.