Question
Question: Figure 3.379...
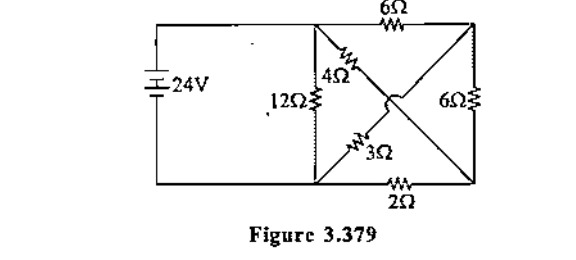
Figure 3.379
89/11 A
Solution
To find the total current drawn from the 24V source, we first need to calculate the equivalent resistance of the entire circuit.
The circuit can be divided into two main parallel branches connected across the 24V source:
- A 12Ω resistor.
- A Wheatstone bridge-like structure.
Let's label the nodes of the bridge:
- Let the positive terminal of the 24V source be P.
- Let the negative terminal of the 24V source be N.
- Let the internal nodes of the bridge be X and Y.
The resistances in the bridge are:
- RPX=6Ω
- RPY=4Ω
- RXN=6Ω
- RYN=2Ω
- RXY=3Ω
First, check if the Wheatstone bridge is balanced:
RPX/RPY=6/4=1.5
RXN/RYN=6/2=3
Since 1.5=3, the bridge is unbalanced, and current flows through the 3Ω resistor (RXY).
To find the equivalent resistance of the unbalanced bridge, we can use a Y-Δ (or Δ-Y) transformation. Let's transform the delta circuit formed by nodes N, X, Y into a star circuit. The resistances in the delta NXY are RXN=6Ω, RYN=2Ω, RXY=3Ω. Let the central node of the equivalent star be O'. The sum of resistances in the delta is 6+2+3=11Ω.
The resistances of the equivalent star arms are:
RO′X=(RXN×RXY)/(RXN+RYN+RXY)
RO′X=(6×3)/11=18/11Ω
RO′Y=(RYN×RXY)/(RXN+RYN+RXY)
RO′Y=(2×3)/11=6/11Ω
RO′N=(RXN×RYN)/(RXN+RYN+RXY)
RO′N=(6×2)/11=12/11Ω
Now, the circuit simplifies:
-
The resistor RPX=6Ω is in series with RO′X=18/11Ω.
RPXO′=RPX+RO′X=6+18/11=(66+18)/11=84/11Ω.
-
The resistor RPY=4Ω is in series with RO′Y=6/11Ω.
RPYO′=RPY+RO′Y=4+6/11=(44+6)/11=50/11Ω.
These two series combinations (RPXO′ and RPYO′) are in parallel with each other.
RParallel_PO′=(RPXO′×RPYO′)/(RPXO′+RPYO′)
RParallel_PO′=((84/11)×(50/11))/((84/11)+(50/11))
RParallel_PO′=(4200/121)/(134/11)
RParallel_PO′=(4200/121)×(11/134)
RParallel_PO′=4200/(11×134)=4200/1474=2100/737Ω.
This parallel combination is in series with RO′N=12/11Ω. So, the equivalent resistance of the bridge section (Rbridge) connected between P and N is:
Rbridge=RParallel_PO′+RO′N
Rbridge=2100/737+12/11
To add these, find a common denominator. 737=11×67.
Rbridge=2100/737+(12×67)/(11×67)
Rbridge=2100/737+804/737=(2100+804)/737=2904/737Ω.
Finally, the 12Ω resistor is in parallel with this Rbridge. The total equivalent resistance of the circuit (Req) is:
1/Req=1/12+1/Rbridge
1/Req=1/12+1/(2904/737)
1/Req=1/12+737/2904
To add these, find a common denominator. 2904=12×242.
1/Req=242/2904+737/2904
1/Req=(242+737)/2904=979/2904
Req=2904/979Ω. We can simplify this fraction. 979=11×89. 2904/11=264. So, Req=264/89Ω.
Now, calculate the total current (I) drawn from the 24V source using Ohm's Law:
I=V/Req
I=24V/(264/89Ω)
I=(24×89)/264
Since 264=24×11:
I=89/11A.
I≈8.09A.
The total current drawn from the 24V source is 89/11A.
Explanation of the solution:
- Identify the circuit components and configuration. The circuit consists of a 24V source, a 12Ω resistor, and a complex network of five resistors forming an unbalanced Wheatstone bridge.
- Recognize that the 12Ω resistor is in parallel with the entire bridge network.
- Analyze the bridge network: It is an unbalanced Wheatstone bridge because the ratio of resistances in adjacent arms is not equal (6/4=6/2).
- Apply a Y-Δ or Δ-Y transformation to simplify the unbalanced bridge. Here, a Δ-Y transformation was applied to the delta formed by the 6Ω, 2Ω, and 3Ω resistors (connected at nodes N, X, Y).
- Calculate the equivalent resistances of the star arms (RO′X, RO′Y, RO′N).
- Redraw the circuit after the transformation. The transformed star resistors are now in series with the other bridge resistors, creating two parallel branches.
- Calculate the equivalent resistance of these two parallel branches.
- Add the equivalent resistance of the parallel branches to the remaining series resistance (RO′N) to find the total equivalent resistance of the bridge (Rbridge).
- Combine Rbridge in parallel with the 12Ω resistor to find the overall equivalent resistance of the circuit (Req).
- Use Ohm's Law (I=V/Req) to calculate the total current drawn from the source.
