Question
Question: Enthalpy, H $Cs^+(g) + F(g)$ $\Delta H_1 = 79.4kJ/mol$ $Cs(g) + \frac{1}{2}F_2(g)$ $\Delta H_2 = 3...
Enthalpy, H
Cs+(g)+F(g) ΔH1=79.4kJ/mol
Cs(g)+21F2(g) ΔH2=375.7kJ/mol
Cs(g)+21F2(g) ΔH3=76.5kJ/mol
Cs(s)+21F2(g) Overall change CsF(s) ΔH4=−328.2kJ/mol
Cs+(g)+F−(g) ΔH5=−756.9kJ/mol
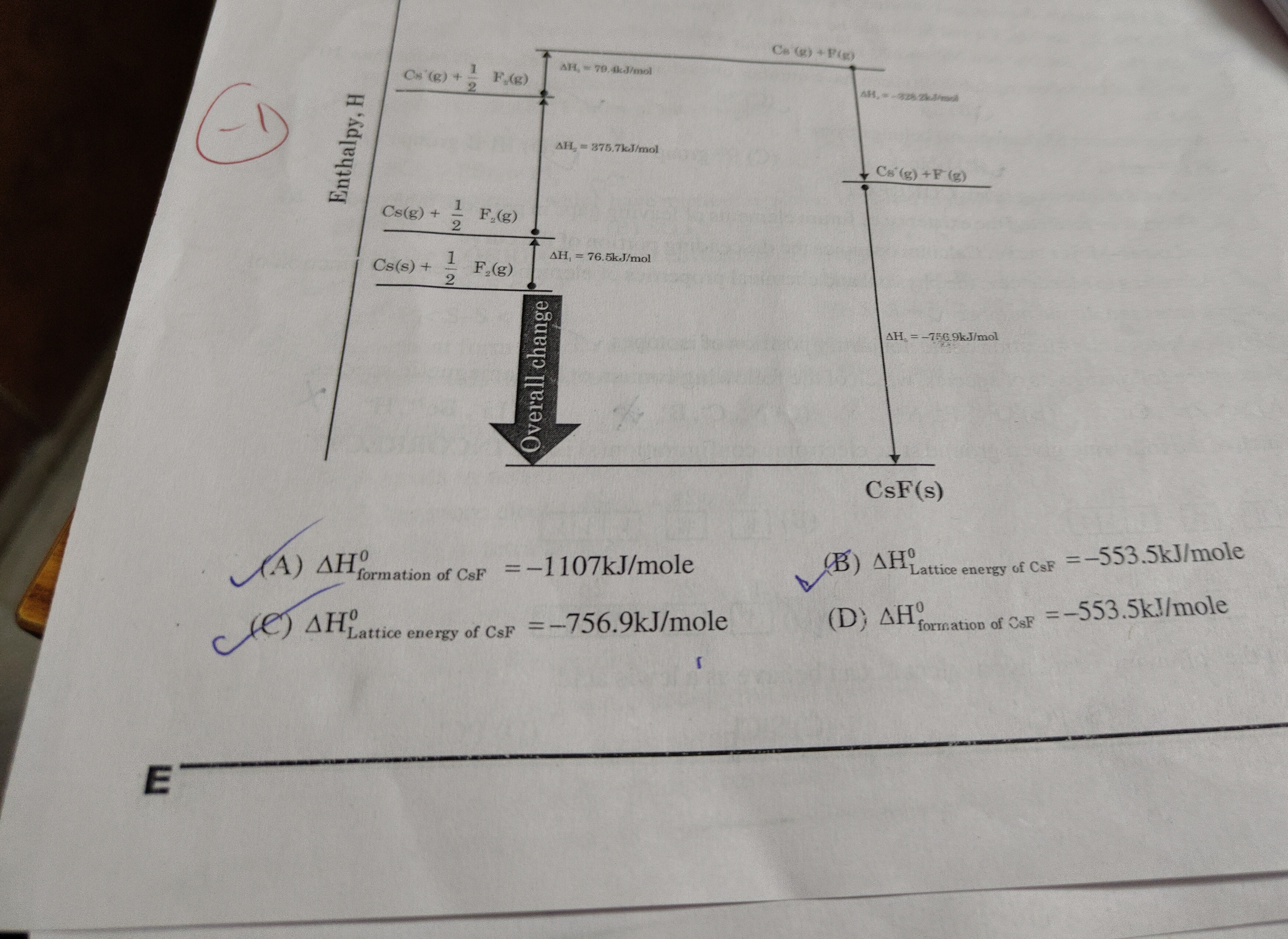
ΔHformationofCsF0=−1107kJ/mole
ΔHLatticeenergyofCsF0=−553.5kJ/mole
ΔHLatticeenergyofCsF0=−756.9kJ/mole
ΔHformationofCsF0=−553.5kJ/mole
C, D
Solution
The Born-Haber cycle is used to calculate the lattice energy or the enthalpy of formation of an ionic compound by applying Hess's Law. The cycle breaks down the formation of an ionic solid from its elements into a series of steps for which the enthalpy changes are known or can be determined.
Let's identify each enthalpy change from the given diagram:
-
Enthalpy of Sublimation of Cesium (ΔHsub):
This is the energy required to convert solid Cesium to gaseous Cesium.
Cs(s)→Cs(g)
From the diagram, the enthalpy change from Cs(s)+21F2(g) to Cs(g)+21F2(g) is ΔH3.
ΔHsub=ΔH3=76.5 kJ/mol -
Ionization Enthalpy of Cesium (IE):
This is the energy required to remove one electron from a gaseous Cesium atom.
Cs(g)→Cs+(g)+e−
From the diagram, the enthalpy change from Cs(g)+21F2(g) to Cs+(g)+21F2(g) is ΔH2.
IE=ΔH2=375.7 kJ/mol -
Bond Dissociation Enthalpy of Fluorine (21BE):
This is the energy required to break the bond in half a mole of gaseous F₂ to form gaseous F atoms.
21F2(g)→F(g)
From the diagram, the enthalpy change from Cs+(g)+21F2(g) to Cs+(g)+F(g) is ΔH1.
21BE=ΔH1=79.4 kJ/mol -
Electron Gain Enthalpy of Fluorine (EGE):
This is the energy change when an electron is added to a gaseous Fluorine atom to form a gaseous Fluoride ion.
F(g)+e−→F−(g)
From the diagram, the enthalpy change from Cs+(g)+F(g) to Cs+(g)+F−(g) is ΔH4.
EGE=ΔH4=−328.2 kJ/mol -
Lattice Energy of Cesium Fluoride (LE):
This is the energy released when gaseous Cesium ions and gaseous Fluoride ions combine to form one mole of solid Cesium Fluoride.
Cs+(g)+F−(g)→CsF(s)
From the diagram, the enthalpy change from Cs+(g)+F−(g) to CsF(s) is ΔH5.
LE=ΔH5=−756.9 kJ/mol
Now let's evaluate the given options:
(C) ΔHLatticeenergyofCsF0=−756.9 kJ/mole
As identified above, the lattice energy (LE) is directly given as ΔH5=−756.9 kJ/mol.
Therefore, option (C) is correct.
(D) ΔHformationofCsF0=−553.5 kJ/mole
The standard enthalpy of formation (ΔHf0) of CsF is the overall enthalpy change for the reaction:
Cs(s)+21F2(g)→CsF(s)
According to Hess's Law, the overall enthalpy change is the sum of the enthalpy changes of all the individual steps in the Born-Haber cycle:
ΔHf0=ΔHsub+IE+21BE+EGE+LE
ΔHf0=ΔH3+ΔH2+ΔH1+ΔH4+ΔH5
Substituting the values:
ΔHf0=76.5 kJ/mol+375.7 kJ/mol+79.4 kJ/mol+(−328.2 kJ/mol)+(−756.9 kJ/mol)
ΔHf0=531.6 kJ/mol−328.2 kJ/mol−756.9 kJ/mol
ΔHf0=203.4 kJ/mol−756.9 kJ/mol
ΔHf0=−553.5 kJ/mol
Therefore, option (D) is correct.
(A) ΔHformationofCsF0=−1107 kJ/mole
This value is incorrect as calculated above.
(B) ΔHLatticeenergyofCsF0=−553.5 kJ/mole
This value is incorrect. -553.5 kJ/mol is the enthalpy of formation, not the lattice energy.
Based on the calculations, both options (C) and (D) are correct.
