Question

calculate magnetic field, as $Bx \hat{i} + By \hat{j} + Bz \hat{k}$

Answer 1

$\vec{B}=0\,\hat{i}-1.06\times10^{-5}\,\hat{j}+0\,\hat{k}\quad\text{(T)}$

Answer 2

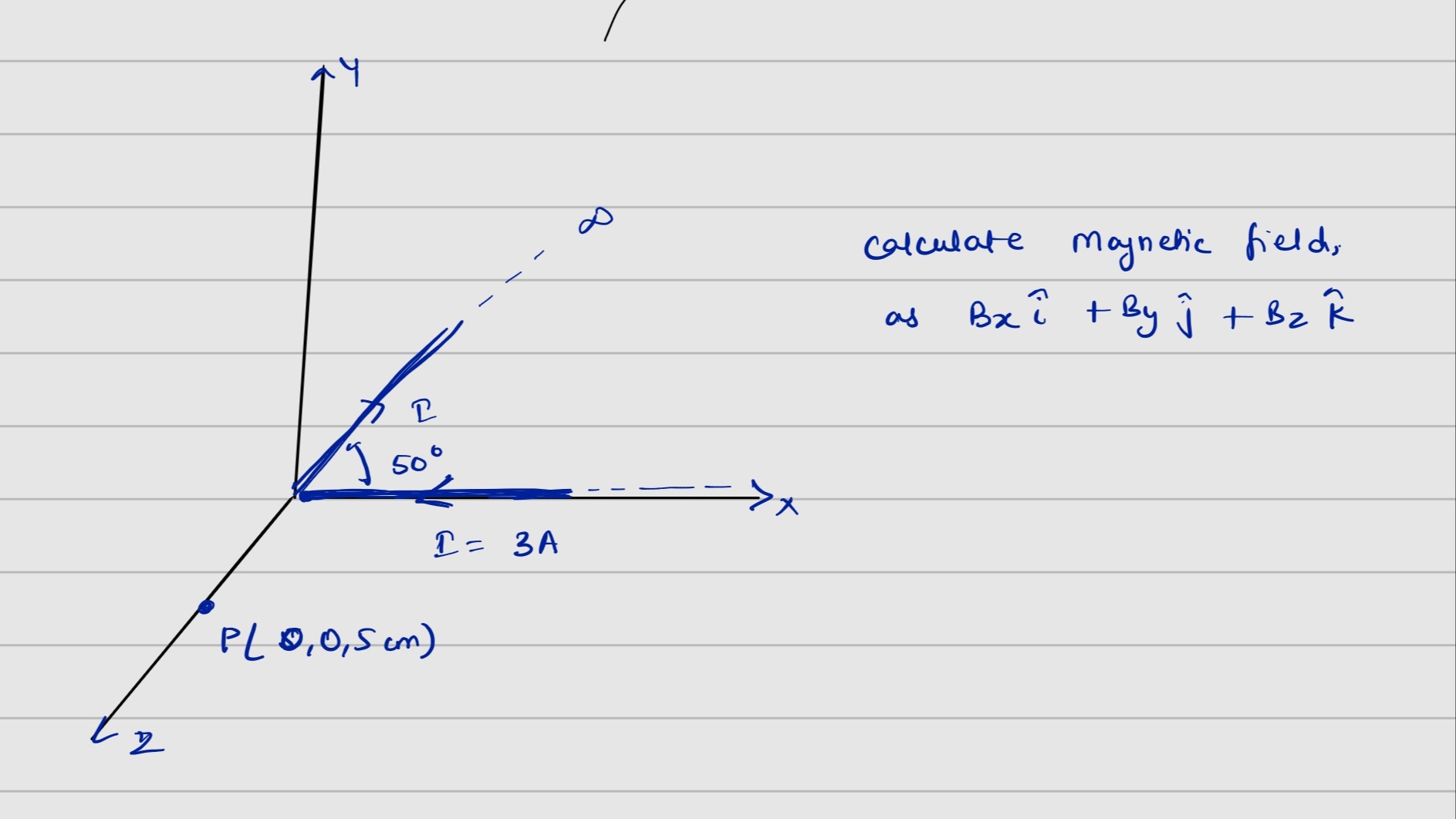
We wish to find the magnetic field at point

$$P(0,0,0.05\,\mathrm{m})$$

in a 3D coordinate system (with $x$ to the right, $y$ upward, and $z$ “downward”). A current $I=3\,A$ flows along the positive $x$–axis. In the diagram a ray labelled “$r$” from the origin makes an angle $50^\circ$ with the $x$–axis. (In the standard formula the two ends of the wire subtend angles $\theta_1$ and $\theta_2$ at $P$; here the lower (finite) end at the origin gives $\theta_1=90^\circ$ since the line joining $P$ to the origin is perpendicular to the $x$–axis, and the other (upper) end gives $\theta_2=50^\circ$.)

For a finite straight conductor the magnetic field at a point located a perpendicular distance $d$ from the wire is

$$B=\frac{\mu_0 I}{4\pi\,d}\Bigl(\sin\theta_1+\sin\theta_2\Bigr)$$

with direction given by the right–hand rule (circling the wire).

Here,

• $d$ is the perpendicular distance from the $x$–axis to $P$. Since $P(0,0,0.05)$ is 0.05 m from the $x$–axis, we have $d=0.05\,\mathrm{m}$.
• $\theta_1=90^\circ$ so $\sin\theta_1=1$.
• $\theta_2=50^\circ$ so $\sin\theta_2\approx0.7660$.

Thus the magnitude is

$$B=\frac{\mu_0 I}{4\pi\,(0.05)}\Bigl(1+0.7660\Bigr) =\frac{(4\pi\times10^{-7})(3)}{4\pi\,(0.05)}\,(1.7660).$$

Cancel the $4\pi$’s:

$$B=\frac{3\times10^{-7}}{0.05}\,(1.7660).$$

Now,

$$\frac{3\times10^{-7}}{0.05}=6\times10^{-6}\,.$$

Thus,

$$B=6\times10^{-6}\times1.7660\approx1.06\times10^{-5}\,\text{T}.$$

Direction:

For a current along $+\hat{i}$ the magnetic field “circulates” around the wire. At point $P$ (which lies along the $+\hat{k}$ direction relative to the wire) the right–hand rule tells us that the field is in the $-\hat{j}$ direction.

Therefore, the magnetic field at $P$ is:

$$\boxed{\vec{B}=0\,\hat{i}-1.06\times10^{-5}\,\hat{j}+0\,\hat{k}\quad\text{(T)}.}$$

---

Minimal Explanation of the Core Steps

1. Identify that $P$ is at a perpendicular distance $d=0.05\,\text{m}$ from the $x$–axis.
2. Recognize that the conductor is finite – with one end at the origin ($\theta_1=90^\circ$) and the other “end at infinity” or making a $50^\circ$ with the $x$–axis ($\theta_2=50^\circ$).
3. Use

$$B=\frac{\mu_0 I}{4\pi\,d}\Bigl(\sin\theta_1+\sin\theta_2\Bigr)$$

with $\mu_0=4\pi\times10^{-7}\,\text{T·m/A}$. 4. Compute the magnitude and assign the direction (using the right–hand rule, the field at $P$ is along $-\hat{j}$).

---

Final Answer

$$\boxed{\vec{B}=0\,\hat{i}-1.06\times10^{-5}\,\hat{j}+0\,\hat{k}\quad\text{(T)}.}$$