Question

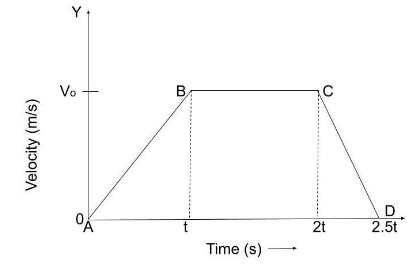
Figure below shows a velocity-time graph for a car starting from rest. The graph has three parts AB, BC and CD. Compare the distance travelled in part BC with the distance travelled in part AB.

Answer 1

Let us first get some idea about the Motion in a straight line. Uniform motion occurs when a body moves in a straight line and covers the same amount of distance in the same period of time. In simple terms, if the rate of change of a body's velocity is constant, it is said to have uniform acceleration.

Complete step by step answer:
The motion of items travelling in a straight line is described using velocity-time graphs. They can be used to calculate displacement and show acceleration. Because the object's velocity is the derivative of its position graph, the area under the line in the velocity vs. time graph represents the object's displacement. (Time is on the x-axis, and velocity is on the y-axis.)

Let us now solve the question:
As we can see that the Distance travelled in part BC $=$ Area of the rectangle tBC2t
$\text{Distance travelled in part BC} =$ Base $\times$ Height
$\Rightarrow \text{Distance travelled in part BC} = \,(2t - t) \times {V_o}$
$\Rightarrow \text{Distance travelled in part BC} = \,{V_o} \times t \\\$
Now, the distance travelled in part AB $=$ Area of the Triangle ABt
$\text{Distance travelled in part AB}= \,\dfrac{1}{2} \times base \times height$
$\therefore \text{Distance travelled in part AB}= \,\dfrac{1}{2} \times t \times {V_o}$

Therefore, the Distance travelled in Part BC : Distance travelled in part AB :: $2:1$.

Note: To solve this kind of question there are some points which we should keep on our finger-tips. In this problem we are using the concept of motion in a straight line, speed and velocity concept and basic concept of area under the curve.