Question
Question: Figure below shows a mass m with a massless inextensible string passing over a frictionless pulley. ...
Figure below shows a mass m with a massless inextensible string passing over a frictionless pulley. The spring constant is k, what is the time period of oscillation of the mass?
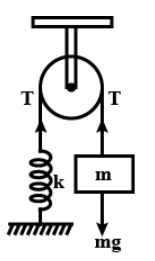
Solution
First, we will equate the tension force with the gravitational force acting on the mass and then we will equate tension with spring force. By doing this we will get a relation between vertical displacement of spring and mass of the body. Then substituting that relation in the formula of time period of oscillation we will get the required answer.
Formula: T=2πgy
Complete answer:
At equilibrium, mass mg will be balanced by the tension force T. Let the vertical displacement of the spring be y. So, the spring force will be balanced by the tension force of the pulley.
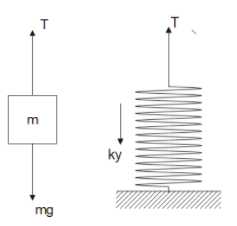
Now, from the free body diagram we can write that T=mg and T=ky
Force acting on the spring is known as restoring force which is given by the formula
F=−ky
Here, k is known as force constant and y is the vertical displacement of spring in this case.
The negative sign in the formula indicates that the force is towards equilibrium position that is towards the equilibrium position.
This restoring force will be equal to tension of the string at equilibrium.
Thus we get,
T=mg=ky
⇒y=kmg
The spring when displaced by a distance ‘y’ will oscillate with a time period of
T=2πgy⇒T=2πgkmg⇒T=2πkm
Additional information:
Whenever a spring is stretched or compressed and then released it will move to and fro around its equilibrium position. This motion of the spring is known as simple harmonic motion (SHM).
The acceleration of the body which performs SHM is given by
a=mF⇒a=m−kyms−2=−ω2y⇒ω=mk
Where ω is the angular frequency of the body.
Note:
In solving such kinds of questions the tension in the strings is always directed away from the respective mass as we know that tension is a pulling force. The spring force acts downwards as it tries to retain its original length that is spring force acts in a direction such that its original length is retained.
