Question
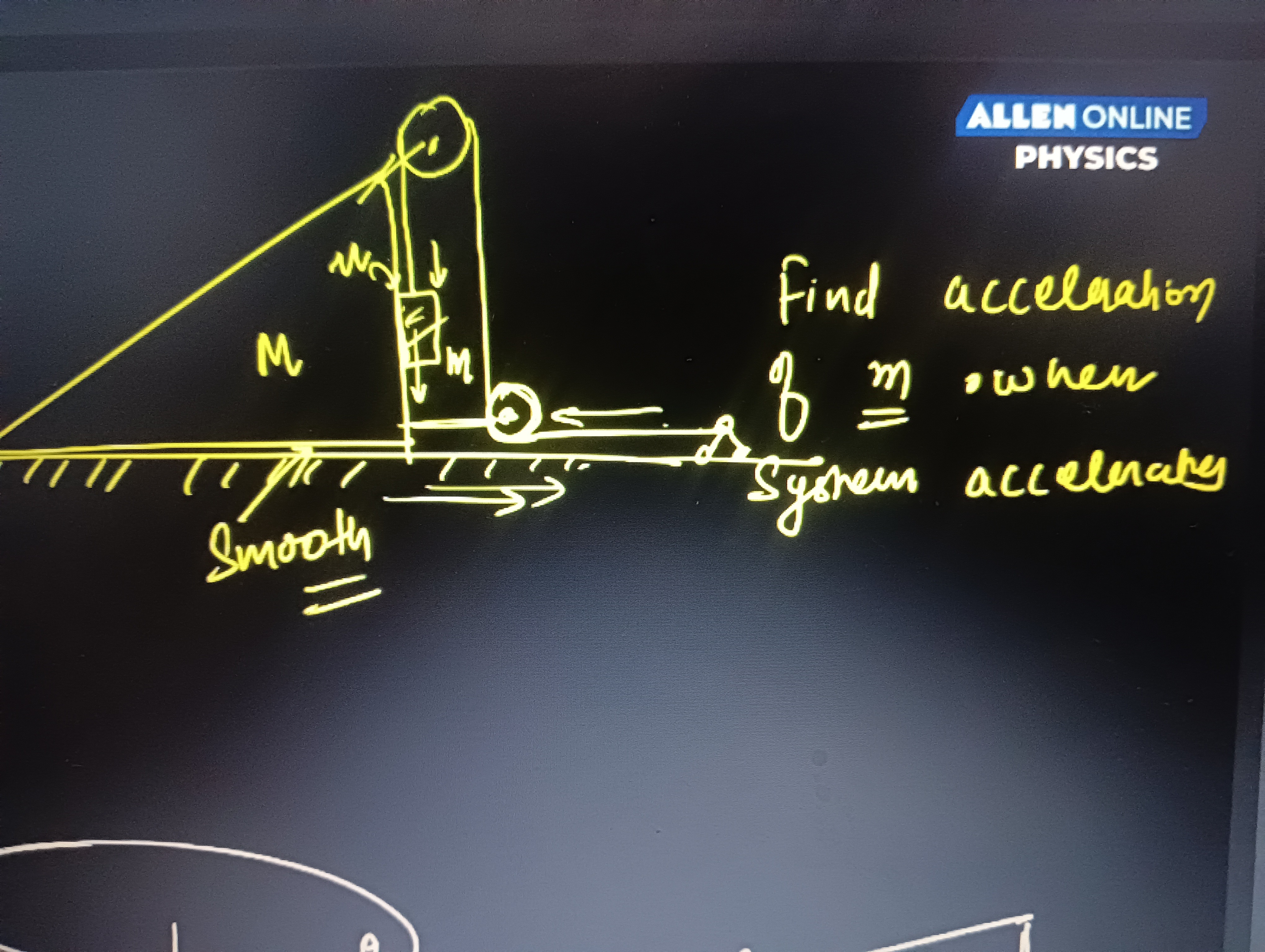
Question: Find acceleration of m when system accelerates. M m Smooth...
Find acceleration of m when system accelerates.
M
m
Smooth
Answer
\frac{mg\sqrt{2}}{M + 2m}
Explanation
Solution
Explanation of the solution:
- Define Accelerations: Let A be the horizontal acceleration of block M. Block m moves along the vertical face of M, so its horizontal acceleration is also A. Let arel be the downward acceleration of m relative to M. The absolute vertical acceleration of m is arel.
- String Constraint: The string connects a fixed point on the ground to the pulley on M, and then to m. The total length of the string is constant. Let xM be the position of M and ym be the vertical position of m. Differentiating the string length equation, L=(xM−xfixed)+(H−ym), twice with respect to time yields 0=aM−ay. Thus, the horizontal acceleration of M (A) is equal to the absolute downward vertical acceleration of m (arel). So, A=arel.
- Free Body Diagrams and Newton's Second Law:
- For block m:
- Vertical forces: mg (downwards), T (upwards). Equation: mg−T=marel=mA.
- Horizontal forces: NM (normal force from M on m, to the right). Equation: NM=mA.
- For block M:
- Horizontal forces: T (from horizontal string, to the right), Nm (normal force from m on M, to the left). By Newton's third law, Nm=NM. Equation: T−NM=MA.
- For block m:
- Solve the System of Equations:
- From NM=mA, substitute into the equation for M: T−mA=MA⟹T=(M+m)A.
- Substitute T into the equation for m: mg−(M+m)A=mA.
- Rearrange and solve for A: mg=mA+MA+mA=(M+2m)A⟹A=M+2mmg.
- Acceleration of m: Block m has a horizontal acceleration A and a vertical acceleration A. The magnitude of its total acceleration is am=A2+A2=A2.
- Final Result: Substitute the value of A: am=M+2mmg2.
The final answer is M+2mmg2.
