Question

• A. $\left(\frac{E_1+E_2}{C_1+C_2}\right)C_2$
• B. $\left(\frac{E_1-E_2}{C_1+C_2}\right)C_2$
• C. $\left(\frac{E_1+E_2}{C_1+C_2}\right)C_1$
• D. $\left(\frac{E_1-E_2}{C_1+C_2}\right)C_1$

Answer 1

Answer: (D)

$\left(\frac{E_1-E_2}{C_1+C_2}\right)C_1$

Answer 2

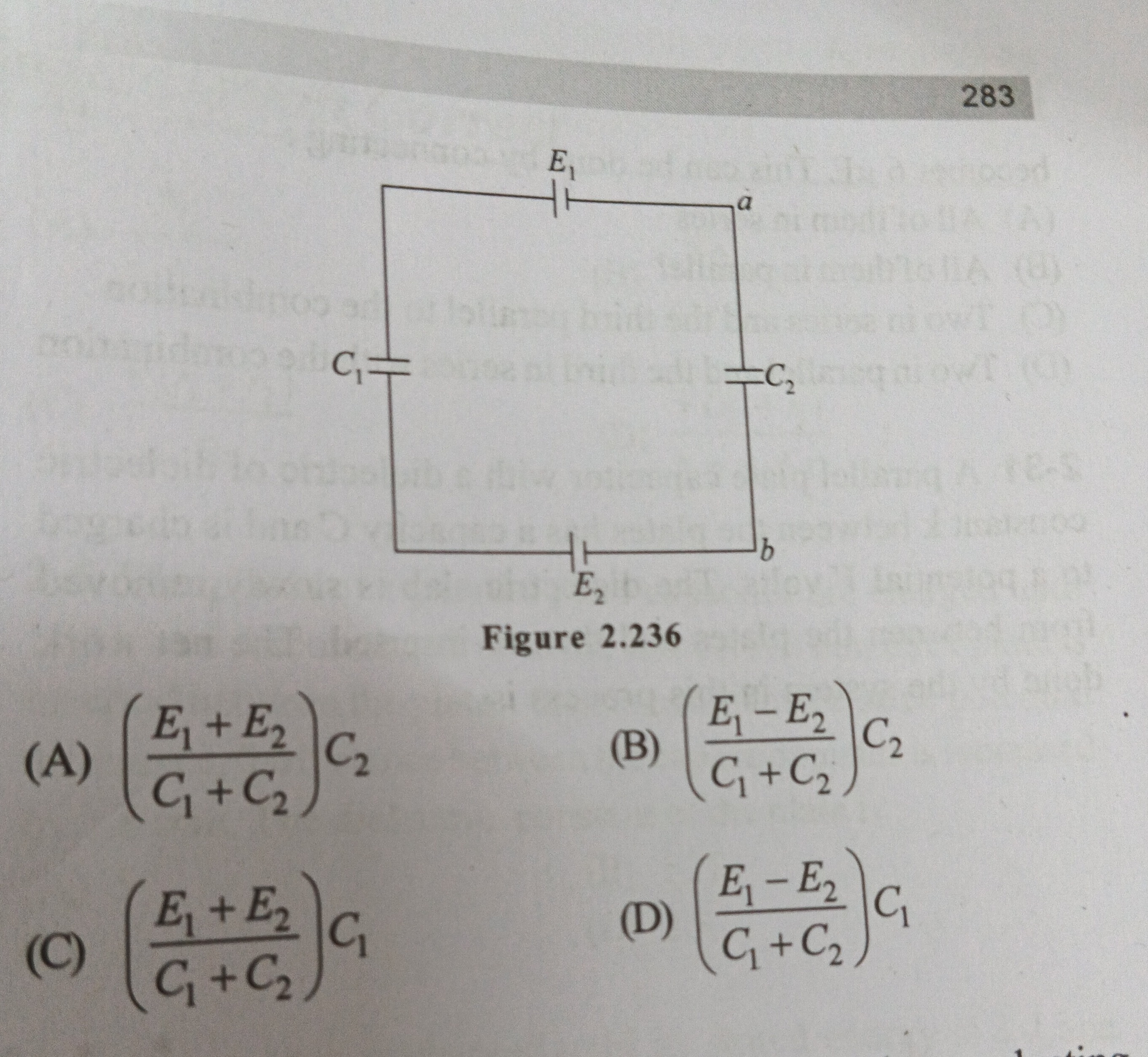
The problem asks for the potential difference between points 'a' and 'b' in the given circuit. The circuit consists of two capacitors $C_1$ and $C_2$, and two batteries $E_1$ and $E_2$, arranged in a closed loop.

To solve this, we apply the superposition principle, a valid method for linear circuits like those with capacitors and batteries. We consider the effect of each battery acting alone and then combine the results.

1. Effect of $E_1$ alone (short $E_2$):

   The circuit becomes a series combination of $C_1$ and $C_2$ connected across $E_1$. The equivalent capacitance is $C_{eq} = \frac{C_1 C_2}{C_1+C_2}$. The charge on each capacitor is $Q = E_1 C_{eq} = E_1 \frac{C_1 C_2}{C_1+C_2}$. The potential difference across $C_2$ (which is $V_a - V_b$ due to $E_1$) is $V_{C2, E1} = Q/C_2 = \frac{E_1 C_1 C_2}{(C_1+C_2)C_2} = \frac{E_1 C_1}{C_1+C_2}$.

2. Effect of $E_2$ alone (short $E_1$):

   The circuit becomes a series combination of $C_1$ and $C_2$ connected across $E_2$. The equivalent capacitance is $C_{eq} = \frac{C_1 C_2}{C_1+C_2}$. The charge on each capacitor is $Q' = E_2 C_{eq} = E_2 \frac{C_1 C_2}{C_1+C_2}$. Now, consider the direction. $E_2$ drives charge in the opposite direction compared to $E_1$ for $V_a-V_b$. The positive terminal of $E_2$ is at 'b'. So, $V_b$ is higher than $V_Y$. The potential difference across $C_2$ is $V_a - V_b$. If $E_2$ is the only source, it will charge $C_2$ such that $V_b > V_a$ (positive charge on lower plate of $C_2$). So, $V_b - V_a = Q'/C_2 = \frac{E_2 C_1 C_2}{(C_1+C_2)C_2} = \frac{E_2 C_1}{C_1+C_2}$. Therefore, $V_{a} - V_{b}$ due to $E_2$ alone is $V_{C2, E2} = -\frac{E_2 C_1}{C_1+C_2}$.

3. Total potential difference:

   $V_a - V_b = V_{C2, E1} + V_{C2, E2} = \frac{E_1 C_1}{C_1+C_2} - \frac{E_2 C_1}{C_1+C_2}$. $V_a - V_b = \frac{(E_1 - E_2) C_1}{C_1+C_2}$.

Therefore, the final answer is $\left(\frac{E_1-E_2}{C_1+C_2}\right)C_1$.