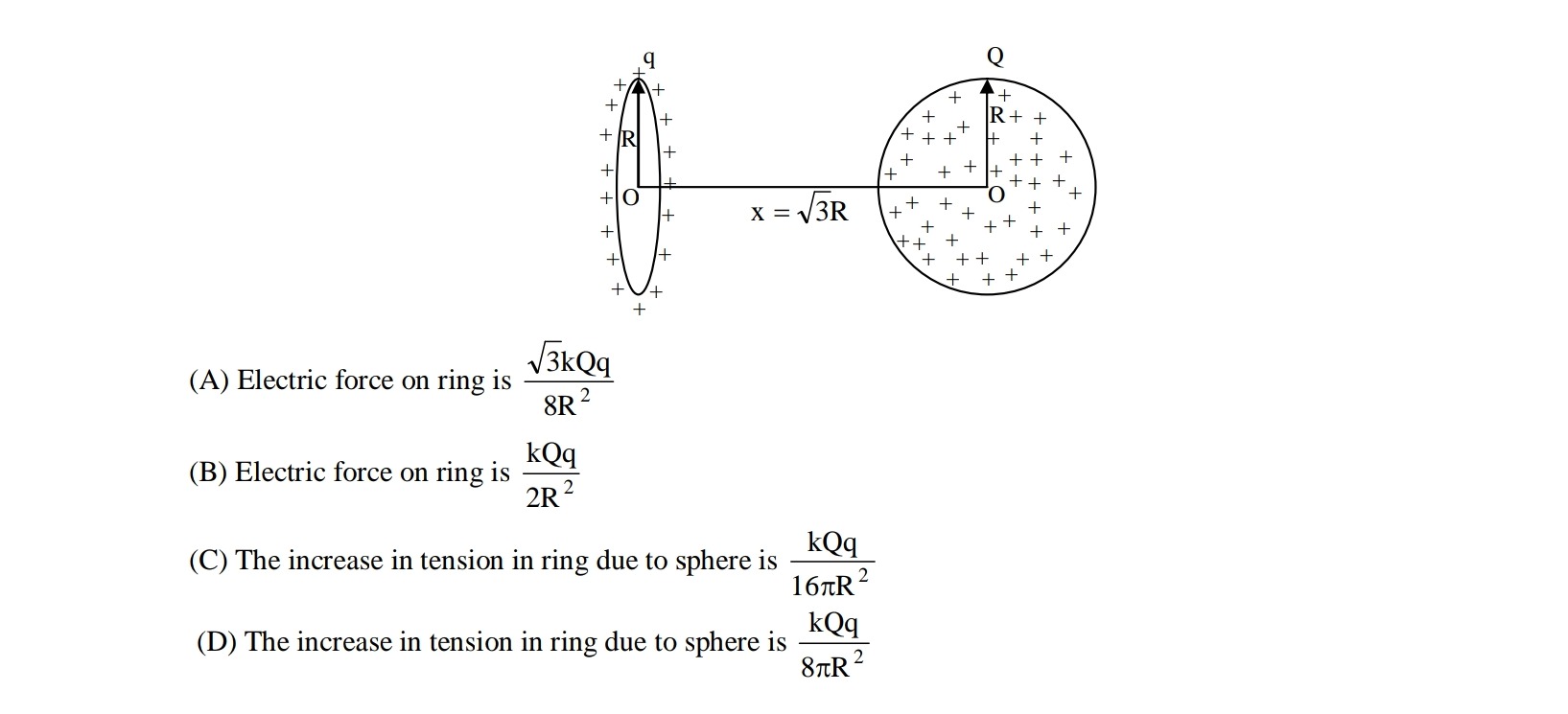
Question

(A) Electric force on ring is $\frac{\sqrt{3}kQq}{8R^2}$

(B) Electric force on ring is $\frac{kQq}{2R^2}$

(C) The increase in tension in ring due to sphere is $\frac{kQq}{16\pi R^2}$

(D) The increase in tension in ring due to sphere is $\frac{kQq}{8\pi R^2}$

• A. Electric force on ring is $\frac{\sqrt{3}kQq}{8R^2}$
• B. Electric force on ring is $\frac{kQq}{2R^2}$
• C. The increase in tension in ring due to sphere is $\frac{kQq}{16\pi R^2}$
• D. The increase in tension in ring due to sphere is $\frac{kQq}{8\pi R^2}$

Answer 1

Answer: (A), (C)

A, C

Answer 2

The problem asks for two quantities: the electric force on the ring due to the sphere, and the increase in tension in the ring due to the sphere.

1. Electric force on the ring due to the sphere:

According to Newton's third law, the force on the ring due to the sphere is equal in magnitude and opposite in direction to the force on the sphere due to the ring. It is often easier to calculate the force on the sphere due to the ring.

The electric field produced by a uniformly charged ring of radius $R$ and total charge $q$ at a distance $x$ along its axis from its center is given by:

$E_{ring} = \frac{k q x}{(R^2 + x^2)^{3/2}}$

In this problem, the center of the sphere is located at a distance $x = \sqrt{3}R$ from the center of the ring. So, the electric field produced by the ring at the center of the sphere is:

$E_{ring} = \frac{k q (\sqrt{3}R)}{(R^2 + (\sqrt{3}R)^2)^{3/2}}$ $E_{ring} = \frac{k q \sqrt{3}R}{(R^2 + 3R^2)^{3/2}}$ $E_{ring} = \frac{k q \sqrt{3}R}{(4R^2)^{3/2}}$ $E_{ring} = \frac{k q \sqrt{3}R}{(2R)^3}$ $E_{ring} = \frac{k q \sqrt{3}R}{8R^3}$ $E_{ring} = \frac{k q \sqrt{3}}{8R^2}$

The force on the sphere (which has charge $Q$) due to this electric field is:

$F_{sphere} = Q E_{ring} = Q \left(\frac{k q \sqrt{3}}{8R^2}\right) = \frac{\sqrt{3}k Q q}{8R^2}$

By Newton's third law, the electric force on the ring due to the sphere is equal in magnitude to $F_{sphere}$.

Thus, the electric force on the ring is $\frac{\sqrt{3}k Q q}{8R^2}$.

This matches option (A).

2. Increase in tension in the ring due to the sphere:

To find the increase in tension, we need to consider the radial outward force exerted by the sphere on each element of the ring.

For an external point, a uniformly charged sphere behaves like a point charge located at its center. So, the sphere with charge $Q$ can be treated as a point charge $Q$ at its center.

Let's find the distance from the center of the sphere to any point on the ring. The center of the sphere is at $x = \sqrt{3}R$ from the center of the ring. The radius of the ring is $R$. Any point on the ring is at a distance $R$ from the ring's center and is perpendicular to the axis.

The distance from the center of the sphere to any point on the ring, $r'$, can be found using the Pythagorean theorem:

$r' = \sqrt{x^2 + R^2} = \sqrt{(\sqrt{3}R)^2 + R^2} = \sqrt{3R^2 + R^2} = \sqrt{4R^2} = 2R$.

So, every point on the ring is at a distance $2R$ from the center of the sphere.

The electric field produced by the sphere at any point on the ring is:

$E' = \frac{k Q}{(r')^2} = \frac{k Q}{(2R)^2} = \frac{k Q}{4R^2}$

This electric field is directed radially outwards from the center of the sphere.

Now, consider a small charge element $dq$ on the ring. The force on this element is $dF = E' dq$.

This force $dF$ acts along the line connecting the center of the sphere to the element $dq$.

Let $\theta$ be the angle between the axis (line connecting the centers of the ring and sphere) and the line connecting the center of the sphere to the element $dq$.

From the geometry, $\cos\theta = \frac{x}{r'} = \frac{\sqrt{3}R}{2R} = \frac{\sqrt{3}}{2}$, which means $\theta = 30^\circ$.

The component of the force $dF$ that is perpendicular to the axis and directed radially outwards from the center of the ring is $dF_r = dF \sin\theta$. This radial component contributes to the tension in the ring.

$dF_r = (E' dq) \sin\theta = \left(\frac{k Q}{4R^2} dq\right) \sin(30^\circ)$ $dF_r = \frac{k Q}{4R^2} dq \left(\frac{1}{2}\right) = \frac{k Q}{8R^2} dq$

The charge $dq$ on a small length $dl$ of the ring is $dq = \lambda dl$, where $\lambda = \frac{q}{2\pi R}$ is the linear charge density of the ring.

So, $dF_r = \frac{k Q}{8R^2} \left(\frac{q}{2\pi R} dl\right) = \frac{k Q q}{16\pi R^3} dl$.

The radial force per unit length on the ring, $f_r$, is $\frac{dF_r}{dl}$:

$f_r = \frac{k Q q}{16\pi R^3}$

For a ring of radius $R$ subjected to a uniform outward radial force per unit length $f_r$, the tension $T$ developed in the ring is given by the formula:

$T = f_r R$

So, the increase in tension in the ring due to the sphere is:

$\Delta T = \left(\frac{k Q q}{16\pi R^3}\right) R = \frac{k Q q}{16\pi R^2}$

This matches option (C).

Since both (A) and (C) are correct, this is a multiple-choice question with multiple correct options.