Question
Question: Figure (a), (b) and (c) show three cylindrical copper conductors along with their face areas and len...
Figure (a), (b) and (c) show three cylindrical copper conductors along with their face areas and length. Which geometry will have the highest resistance?
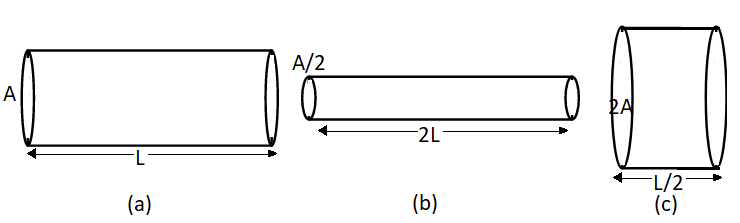
Solution
The resistance of a material depends directly on the length of the material and inversely on the area of cross section. From the given cylinders, we compare the lengths and the areas of the three cylinders.
Formula used:
The resistance of a material is given as:
R=ρAL
where ρ is the resistivity of the material which depends on the temperature of the material and on the nature of it, l is the length and a is the area of cross-section of the material.
Complete answer:
Considering all the three cylinders one by one and substituting the values in the formula,
(1) For the cylinder in case (a),
R=ρAL
(2) For the cylinder in case (b),
R=ρA/22L=4ρAL
(3) For the cylinder in case (c), the resistance is,
R=ρ2AL/2=ρ4AL
As we compare the three cases, we come to know that the resistance of the cylinder in (b) is maximum as it has twice the length and half the area.
Additional information:
This question provides an example of how the resistance can be decreased while devising a circuit. Increasing the area decreases the resistance and decreasing the length also decreases the resistance. The resistivity of any material happens to be an important intrinsic property of the material. On calculating the resistivity, one can determine the nature of electrical conductivity the material offers.
Note:
Since we are given that all the three cylinders are of the same material, copper so the resistivity for all the cylinders will be the same. Therefore, comparisons can be done solely on the basis of area and lengths. The resistivity depends on temperature and type of the material used.
