Question

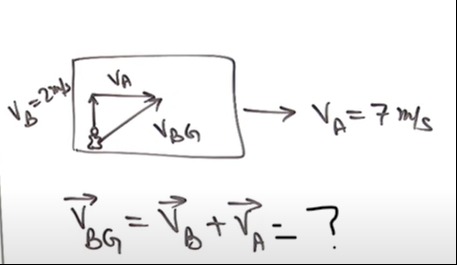
A person walks across a boat with a velocity $\vec{v}_A$ relative to the boat. The boat is moving with a velocity $\vec{v}_B$ relative to the ground. What is the velocity of the person relative to the ground, $\vec{v}_{BG}$?

Answer 1

$\sqrt{53} \, \text{m/s}$

Answer 2

The problem involves the addition of relative velocities. The velocity of the person relative to the ground ($\vec{v}_{BG}$) is the vector sum of the velocity of the person relative to the boat ($\vec{v}_A$) and the velocity of the boat relative to the ground ($\vec{v}_B$). This can be expressed as: $\vec{v}_{BG} = \vec{v}_A + \vec{v}_B$

Given that $\vec{v}_A$ and $\vec{v}_B$ are perpendicular (as implied by typical diagrams for such problems and the context of relative motion where one is horizontal and the other vertical), we can find the magnitude of the resultant velocity using the Pythagorean theorem: $v_{BG}^2 = v_A^2 + v_B^2$

With $v_A = 7 \, \text{m/s}$ and $v_B = 2 \, \text{m/s}$: $v_{BG}^2 = (7 \, \text{m/s})^2 + (2 \, \text{m/s})^2$ $v_{BG}^2 = 49 \, \text{m}^2/\text{s}^2 + 4 \, \text{m}^2/\text{s}^2$ $v_{BG}^2 = 53 \, \text{m}^2/\text{s}^2$

Therefore, the magnitude of the velocity of the person relative to the ground is: $v_{BG} = \sqrt{53} \, \text{m/s}$