Question

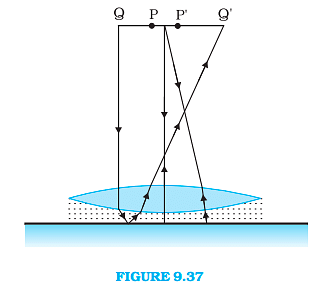
Figure 9.37 shows an equiconvex lens (of refractive index 1.50) in contact with a liquid layer on top of a plane mirror. A small needle with its tip on the principal axis is moved along the axis until its inverted image is found at the position of the needle.

Answer 1

STEP 1:-
In order to find the focal length of the concave lens of liquid :
The formula used will be: $\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}$
In the absence of the liquid, for the combination of the convex lens and plane mirror, the inverted image coincides with the object only when the object is placed at the focus of the convex lens. The same principle applies when the liquid is introduced between the lens and the mirror. Therefore, the given object or image distance can be considered as the focal length of the respective combinations.

When the liquid is present, the system acts as a combination of a convex lens and a concave lens. Hence, the focal length of the combination is denoted as f (let's say): f = 45 cm

When the liquid is removed, the image is formed at 30 cm.
Therefore, the focal length of the convex lens (f1) is: f1 = 30 cm
Let the focal length of the concave lens with the liquid be f2.

For a pair of optical systems in contact, the equivalent focal length is given by:
$\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}$
Putting the values, we get,
$\frac{1}{45}=\frac{1}{30}+\frac{1}{f_2}$
$\frac{1}{f_2}=\frac{1}{45}-\frac{1}{30}$
$\frac{1}{f_2}=\frac{2-3}{90}=-\frac{1}{90}$
$f_2=-90\text{ cm}$

STEP 2:-
In order to find the value of radius of curvature :
Lens makers formula: $\frac{1}{f}=(n_{21}−1)(\frac{1}{R_1}−\frac{1}{R_2})$

Let the refractive index of the lens be n1,
and the radius of curvature of one surface be R1=R.
The radius of curvature of the other surface is R2=-R.

Using the lens makers formula,
$\frac{1}{f}=(n_{21}−1)(\frac{1}{R_1}−\frac{1}{R_2})$
$\frac{1}{30}=(1.5−1)(\frac{1}{R}−\frac{1}{-R})$
$\frac{1}{30}=0.5(\frac{2}{R})$
$\frac{1}{30}=\frac{1}{R}$
$R=30\text{ cm}$

STEP 3:-
In order to find the refractive index of the liquid :
Lens makers formula: $\frac{1}{f}=(n_{21}−1)(\frac{1}{R_1}−\frac{1}{R_2})$

The radius of curvature of the liquid lens, R'1=-30 cm.
The other side of the liquid is a plane, so R'2=∞.
Let n2 be the refractive index of the liquid.

Using the lens maker's formula,
$\frac{1}{f_2}=(n_2−1)(\frac{1}{R_1}−\frac{1}{R_2})$
$−\frac{1}{90}=(n_2−1)(\frac{1}{-30}−\frac{1}{∞})$
$−\frac{1}{90}=−\frac{1}{30}(n_2−1)$
$n_2−1=\frac{1}{3}$
$n_2=1.33$

Hence, the refractive index of the liquid is 1.33.
Therefore, the final Answer: n=1.33