Question

The figure shows a closed loop ABCD carrying a current $I$ in a uniform magnetic field $\vec{B}$ directed horizontally to the right. Find the net force acting on the loop.

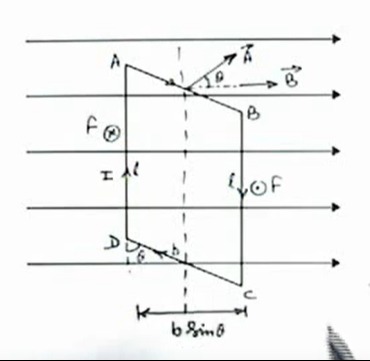
• A. The net force on the loop is $IlB\hat{k}$.
• B. The net force on the loop is $IbB\cos\theta \hat{i}$.
• C. The net force on the loop is zero.
• D. The net force on the loop is $IlB\hat{k} + IbB\cos\theta \hat{i}$.

Answer 1

Answer: (C)

The net force on the loop is zero.

Answer 2

The force on a current-carrying wire segment of length $\vec{l}$ in a magnetic field $\vec{B}$ is given by $\vec{F} = I (\vec{l} \times \vec{B})$. For a closed loop in a uniform magnetic field, the net force is always zero. This is because the vector sum of the forces on individual segments cancels out. Mathematically, for a closed loop, $\oint d\vec{l} = \vec{0}$. Therefore, the net force $\vec{F}_{net} = I \oint d\vec{l} \times \vec{B} = I (\oint d\vec{l}) \times \vec{B} = I (\vec{0}) \times \vec{B} = \vec{0}$.