Question

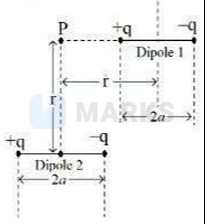
The provided image shows two electric dipoles and a point P. Determine the electric potential at point P.

• A. $\frac{1}{4\pi\epsilon_0} \frac{aq}{\sqrt{2}r^2}$
• B. $-\frac{1}{4\pi\epsilon_0} \frac{aq}{\sqrt{2}r^2}$
• C. $0$
• D. $\frac{1}{4\pi\epsilon_0} \frac{aq}{r^2}$

Answer 1

Answer: (B)

$-\frac{1}{4\pi\epsilon_0} \frac{aq}{\sqrt{2}r^2}$

Answer 2

The problem involves calculating the electric potential at point P due to two electric dipoles. We set up a coordinate system with the center of Dipole 2 at the origin (0,0).

1. Dipole 2: The charges are at (a,0) and (-a,0). Point P is at (0, r). The electric potential at a point on the perpendicular bisector of a dipole is zero. Using the dipole approximation $V = \frac{1}{4\pi\epsilon_0} \frac{\vec{p} \cdot \vec{R}}{R^3}$ for $R \gg a$, where $\vec{p} = 2aq \hat{i}$ and $\vec{R} = r \hat{j}$, we get $V_2 = 0$.

2. Dipole 1: The center of Dipole 1 is at a horizontal distance 'r' from the origin and a vertical distance 'r' from point P. This leads to two possible locations for the center of Dipole 1: (r, 0) or (r, 2r).

   • If the center is at (r, 0), $\vec{p_1} = 2aq \hat{i}$ and $\vec{R_1} = (-r, r)$. Then $V_1 \approx \frac{1}{4\pi\epsilon_0} \frac{(2aq \hat{i}) \cdot (-r \hat{i} + r \hat{j})}{(r\sqrt{2})^3} = \frac{1}{4\pi\epsilon_0} \frac{-2aqr}{2\sqrt{2}r^3} = \frac{1}{4\pi\epsilon_0} \frac{-aq}{\sqrt{2}r^2}$.
   • If the center is at (r, 2r), $\vec{p_1} = 2aq \hat{i}$ and $\vec{R_1} = (-r, -r)$. Then $V_1 \approx \frac{1}{4\pi\epsilon_0} \frac{(2aq \hat{i}) \cdot (-r \hat{i} - r \hat{j})}{(r\sqrt{2})^3} = \frac{1}{4\pi\epsilon_0} \frac{-2aqr}{2\sqrt{2}r^3} = \frac{1}{4\pi\epsilon_0} \frac{-aq}{\sqrt{2}r^2}$.

3. Total Potential: The total potential at P is $V = V_1 + V_2 = V_1 + 0 = -\frac{1}{4\pi\epsilon_0} \frac{aq}{\sqrt{2}r^2}$.