Question

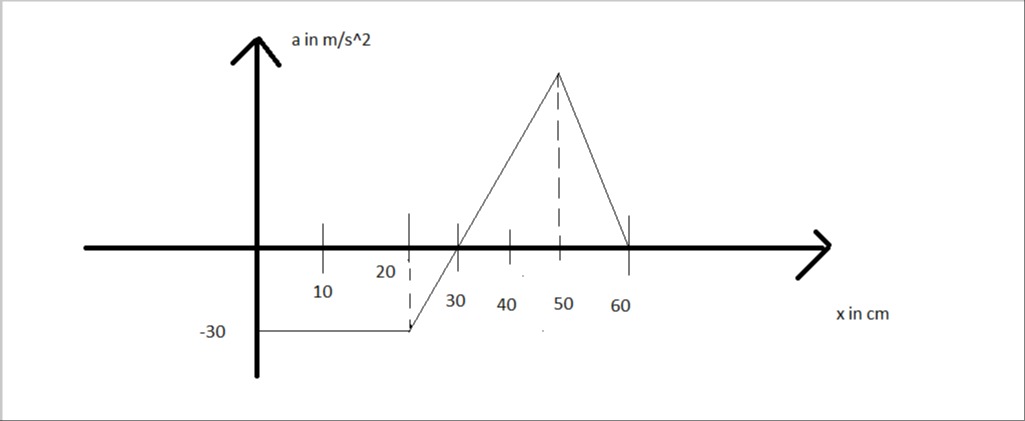
The question is missing from the problem description. However, based on the provided a-x (acceleration-position) graph, a common problem type involves calculating the velocity of an object at a certain position, given its initial velocity. The fundamental relationship used is derived from $a = v \frac{dv}{dx}$, which integrates to:

$\frac{1}{2} v_f^2 - \frac{1}{2} v_i^2 = \int_{x_i}^{x_f} a \, dx$

The integral $\int_{x_i}^{x_f} a \, dx$ represents the area under the a-x graph between positions $x_i$ and $x_f$.

Analysis of the Graph: The x-axis represents position in centimeters (cm), and the y-axis represents acceleration in meters per second squared (m/s²). We must use consistent units, so we convert positions from cm to meters (1 cm = 0.01 m).

• $x=0$ cm = 0 m
• $x=10$ cm = 0.1 m
• $x=20$ cm = 0.2 m
• $x=30$ cm = 0.3 m
• $x=40$ cm = 0.4 m
• $x=50$ cm = 0.5 m
• $x=60$ cm = 0.6 m

The graph can be divided into three segments:

1. From $x=0$ m to $x=0.2$ m: The acceleration is constant at $a = -30$ m/s². Area 1 = Base × Height = $(0.2 - 0) \times (-30) = 0.2 \times (-30) = -6.0 \text{ m}^2/\text{s}^2$.

2. From $x=0.2$ m to $x=0.4$ m: The acceleration changes linearly from $a = -30$ m/s² to $a = 0$ m/s². This forms a trapezoid. Area 2 = $\frac{1}{2} (\text{sum of parallel sides}) \times \text{height (change in x)}$ Area 2 = $\frac{1}{2} (-30 + 0) \times (0.4 - 0.2) = \frac{1}{2} (-30) \times 0.2 = -15 \times 0.2 = -3.0 \text{ m}^2/\text{s}^2$.

3. From $x=0.4$ m to $x=0.6$ m: This segment forms a triangle with its base on the x-axis. The acceleration is 0 at $x=0.4$ m and $x=0.6$ m. The peak of the triangle is at $x=0.5$ m. The value of the peak acceleration is not explicitly given. Let's assume the peak acceleration is $+30$ m/s² for illustrative purposes. Area 3 = Area of triangle = $\frac{1}{2} \times \text{base} \times \text{height}$ Area 3 = $\frac{1}{2} \times (0.6 - 0.4) \times 30 = \frac{1}{2} \times 0.2 \times 30 = 0.1 \times 30 = 3.0 \text{ m}^2/\text{s}^2$.

Hypothetical Question and Solution: Let's assume the question is: "An object starts from rest ($v_i = 0$) at $x_i = 0$. What is its velocity at $x_f = 40$ cm (0.4 m)?"

Using the formula: $\frac{1}{2} v_f^2 - \frac{1}{2} v_i^2 = \int_{x_i}^{x_f} a \, dx$ $\frac{1}{2} v_f^2 - 0 = \text{Area from } x=0 \text{ to } x=0.4 \text{ m}$ The total area from $x=0$ to $x=0.4$ m is Area 1 + Area 2 = $-6.0 + (-3.0) = -9.0 \text{ m}^2/\text{s}^2$.

So, $\frac{1}{2} v_f^2 = -9.0 \text{ m}^2/\text{s}^2$. $v_f^2 = -18.0 \text{ m}^2/\text{s}^2$.

This result yields an imaginary velocity, which is physically impossible for a real object. This indicates that if the object starts from rest at $x=0$, it cannot reach $x=0.4$ m under the described acceleration profile, or the problem statement/graph implies conditions that prevent it.

If the question were about work done, for an object of mass $m$: Work Done $W = m \times \int a \, dx$. For example, if $m=1$ kg and the question asked for work done from $x=0$ to $x=0.4$ m: $W = 1 \text{ kg} \times (-9.0 \text{ m}^2/\text{s}^2) = -9.0 \text{ Joules}$.

Answer 1

The question is missing. Without the specific question, the answer cannot be determined. If we assume a question like "Find the velocity at x=40 cm starting from rest, with peak acceleration +30 m/s²", the result is physically impossible ($v^2 = -18$ m²/s²).

Answer 2

The change in kinetic energy is equal to the area under the a-x graph: $\Delta (\frac{1}{2}mv^2) = m \int a \, dx$. For velocity, $\Delta (\frac{1}{2}v^2) = \int a \, dx$. Calculate the area under the given a-x graph between the initial and final positions. Convert units to be consistent (e.g., meters for position). Use $\frac{1}{2} v_f^2 - \frac{1}{2} v_i^2 = \text{Area}$ to find the final velocity. If the result for $v_f^2$ is negative, it implies a physically impossible scenario under the given conditions, meaning the object cannot reach that position starting from rest.