Question
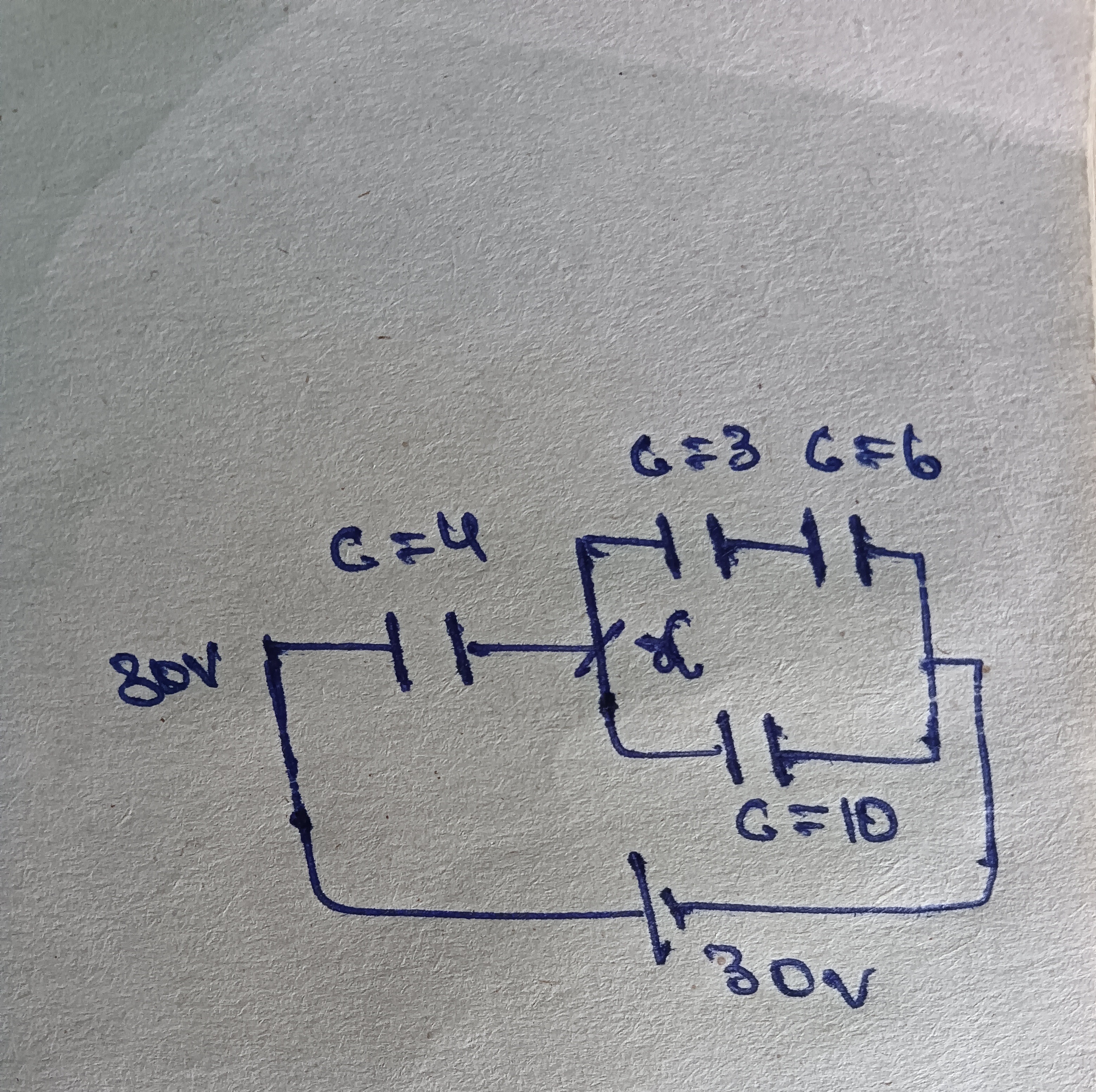
Question: 80V C=4 C=3 C=6 C=10 30V...
80V C=4 C=3 C=6 C=10 30V
Charge on C=4 is 150 μC, C=3 is 25 μC, C=6 is 25 μC, C=10 is 125 μC
Charge on C=4 is 125 μC, C=3 is 25 μC, C=6 is 25 μC, C=10 is 150 μC
Charge on C=4 is 150 μC, C=3 is 150 μC, C=6 is 150 μC, C=10 is 150 μC
Charge on C=4 is 37.5 μC, C=3 is 12.5 μC, C=6 is 12.5 μC, C=10 is 12.5 μC
Charge on C=4 is 150 μC, C=3 is 25 μC, C=6 is 25 μC, C=10 is 125 μC
Solution
The circuit is analyzed by assigning potentials to nodes. The common negative terminal of the voltage sources is set to 0V. The positive terminals are at 80V and 30V respectively. A junction X connects the 4µF capacitor to the parallel combination of capacitors. Charge conservation at node X (Q1=Qp) is used to find the potential VX. The charges on individual capacitors are then calculated using Q=CV and the principle of charge distribution in series and parallel combinations.
The equivalent capacitance of the parallel combination of C=3 and C=6 in series is C23=3+63×6=2. This is in parallel with C=10, so the total parallel capacitance is Cp=2+10=12. Let VX be the potential at the junction. Charge on C=4: Q1=4(80−VX). Charge on Cp: Qp=12(VX−30). By charge conservation, Q1=Qp: 4(80−VX)=12(VX−30) 320−4VX=12VX−360 680=16VX VX=42.5V.
Charges: Q(C=4)=4(80−42.5)=4(37.5)=150μC. The voltage across the parallel combination is Vp=VX−30=42.5−30=12.5V. Q(C=10)=Cp×Vp=10×12.5=125μC. The charge on the series combination C23 is Q23=C23×Vp=2×12.5=25μC. Since C=3 and C=6 are in series, Q(C=3)=Q(C=6)=Q23=25μC.
