Question

In steady state, the capacitor acts as an open circuit. Let the potential at the bottom wire be 0. Consider the left branch: The battery $\epsilon$ is in series with switch $S_1$ and resistor $R$. This combination is connected to a junction point A. In steady state, the current flowing from the battery $\epsilon$ towards A is $I_1$. The potential at A due to this branch is $V_A = \epsilon - I_1 R$. Consider the right branch: Switch $S_2$ is in series with resistor $R$, and this combination is connected to the positive terminal of battery $2\epsilon$. The negative terminal of $2\epsilon$ is connected to the bottom wire. This entire branch is also connected to the junction point A. In steady state, the current flowing from the battery $2\epsilon$ towards A is $I_2$. The potential at A due to this branch is $V_A = 2\epsilon - I_2 R$. The capacitor $C$ is connected between point A and the bottom wire (potential 0). So, the voltage across the capacitor is $V_C = V_A$. Since there is no current flowing through the capacitor in steady state, the current entering point A from the left branch must be equal to the current leaving point A towards the right branch (or vice-versa, depending on the direction of current flow). However, the diagram implies that both branches are connected to point A.

Answer 1

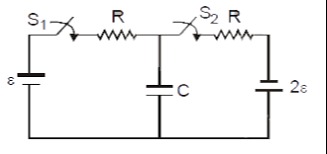
The potential at point A is determined by the parallel combination of the two branches connected to it. In steady state, no current flows through the capacitor, so it acts as an open circuit. Applying Kirchhoff's voltage law to the left loop: $\epsilon - I_1 R - V_C = 0$. Applying Kirchhoff's voltage law to the right loop: $2\epsilon - I_2 R - V_C = 0$. Since the branches are connected to a common point A, and the capacitor is between A and ground, the voltage $V_A$ is the same for both branches. If we assume the current flows from $\epsilon$ through $R$ to A, and from A through $R$ to $2\epsilon$: $V_A = \epsilon - IR$ and $V_A = 2\epsilon + IR$. Equating these gives $\epsilon - IR = 2\epsilon + IR \implies 2IR = -\epsilon \implies IR = -\epsilon/2$. Substituting this back into the first equation: $V_A = \epsilon - (-\epsilon/2) = 3\epsilon/2$. Therefore, the voltage across the capacitor is $V_C = V_A = 3\epsilon/2$. The charge on the capacitor is $Q = C V_C = C (3\epsilon/2)$.

Answer 2

In steady state, the capacitor acts as an open circuit, meaning no current flows through it. We need to determine the potential at point A, where the two branches connect, to find the voltage across the capacitor.

Let's assume the bottom wire is at 0 potential.

Left Branch Analysis: The left branch consists of a voltage source $\epsilon$ in series with a resistor $R$. Let $I_1$ be the current flowing from the positive terminal of $\epsilon$ towards point A. The potential at point A, considering only this branch, can be expressed using Kirchhoff's voltage law: $V_A = \epsilon - I_1 R$

Right Branch Analysis: The right branch consists of a resistor $R$ in series with a voltage source $2\epsilon$. Let $I_2$ be the current flowing from the positive terminal of $2\epsilon$ towards point A. The potential at point A, considering only this branch, can be expressed using Kirchhoff's voltage law: $V_A = 2\epsilon - I_2 R$

Steady State Condition: In steady state, no current flows through the capacitor. This means that the total current entering junction A must equal the total current leaving junction A. Assuming currents $I_1$ and $I_2$ are directed towards A from their respective sources, and no current flows through the capacitor, the net current at A is $I_1 + I_2 = 0$. This implies $I_1 = -I_2$. This means that if current flows from $\epsilon$ towards A, then current must flow from $2\epsilon$ away from A, or vice-versa.

A more common interpretation, and one that leads to a solvable problem, is to consider the potential at point A as the result of these two branches connected in parallel to A. Let's assume the current flows from the higher potential source towards the lower potential source, or that the current from each source flows through its respective resistor to point A.

Let's assume the current $I$ flows from the $\epsilon$ source, through $R$, to point A, and then from point A, through the other $R$, towards the $2\epsilon$ source. Applying KVL to the left loop: $\epsilon - I R - V_A = 0 \implies V_A = \epsilon - IR$

Applying KVL to the right loop (going from A towards the $2\epsilon$ source): $V_A - I R - 2\epsilon = 0 \implies V_A = 2\epsilon + IR$

Equating the two expressions for $V_A$: $\epsilon - IR = 2\epsilon + IR$ $\epsilon - 2\epsilon = IR + IR$ $-\epsilon = 2IR$ $IR = -\frac{\epsilon}{2}$

Now, substitute this value back into the equation for $V_A$: $V_A = \epsilon - IR = \epsilon - (-\frac{\epsilon}{2}) = \epsilon + \frac{\epsilon}{2} = \frac{3\epsilon}{2}$

The voltage across the capacitor, $V_C$, is equal to the potential at point A, since the other side of the capacitor is at ground (0V). $V_C = V_A = \frac{3\epsilon}{2}$

The charge on the capacitor is given by $Q = C V_C$. $Q = C \left(\frac{3\epsilon}{2}\right)$