Question

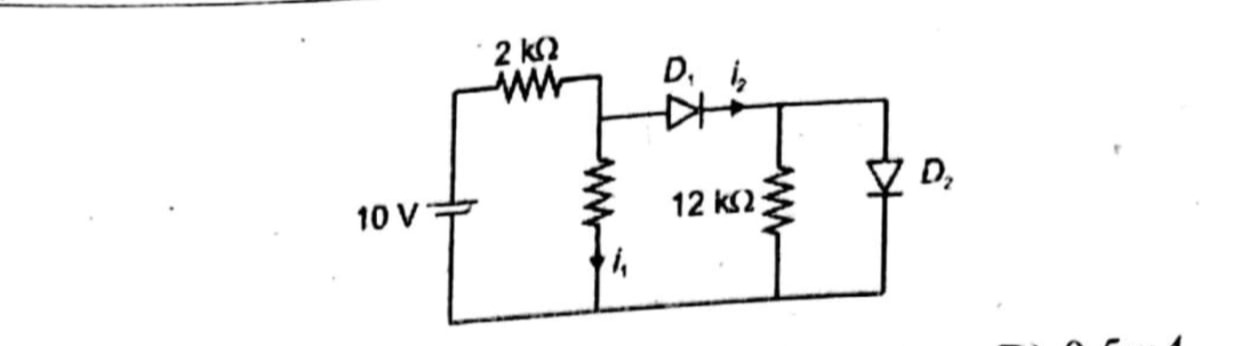
In the circuit shown, all diodes are ideal. A 10 V source is connected in series with a 2 kΩ resistor feeding node A. From node A, there is a vertical resistor down to ground carrying current I₁, and an ideal diode D₁ leading to node B. From node B, a 12 kΩ resistor goes to ground carrying current I₂, and another ideal diode D₂ connects node B to ground. Determine the currents I₁ and I₂.

Answer 1

$I_1 = 2\,\text{mA},\quad I_2 = 0$

Answer 2

Step 1: Identify diode states

• D₂ is forward-biased only if VB>0, but since an ideal diode to ground clamps VB at 0 V, D₂ conducts and VB=0.
• D₁ then sees VA≥VB=0, so D₁ is forward-biased and VA=VB=0.

Step 2: Node voltages

• VB=0 V (clamped by D₂).
• VA=VB (through ideal D₁) = 0 V.

Step 3: Currents

• I₁ flows through the resistor from node A to ground:
  $I_1=\frac{V_A-0}{R_{\text{vertical}}}=\frac{0}{2\,\text{k}\Omega}=0.$
• But the current through the 2 kΩ from the 10 V source into node A must go into I₁ (vertical) plus diode D₁:
  $I_{\text{source}}=\frac{10-0}{2\,\text{k}}=5\,\text{mA}.$
  Since D₁ is ideal and VA=VB=0, all 5 mA flows through D₁ to node B, but at B it splits: one part I₂ through 12 kΩ, the rest through D₂ to ground.
• VB=0 gives
  $I_2=\frac{V_B-0}{12\,\text{k}}=0.$
• Hence all 5 mA from D₁ goes through D₂ to ground, and I₁=0.

Answer:
I₁=0, I₂=0. (All source current bypasses vertically and through 12 kΩ because nodes are at 0 V.)