Question

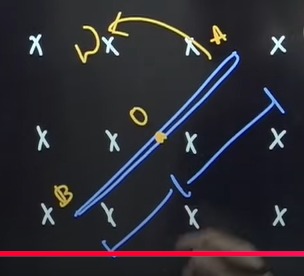
The problem describes a conducting rod OA of length $L$ rotating with a constant angular velocity $\omega$ about an axis passing through its end O, perpendicular to the plane of rotation. A uniform magnetic field $\vec{B}$ is present, directed perpendicular to the plane of rotation (into the page, as indicated by 'x'). We need to find the motional electromotive force (EMF) induced across the rod OA.

Answer 1

$\frac{1}{2} B \omega L^2$

Answer 2

The rod OA of length $L$ rotates with angular velocity $\omega$ in a uniform magnetic field $B$ perpendicular to its plane.

Consider an element $dr$ at distance $r$ from O. Its velocity is $v = r\omega$.

The motional EMF across this element is $d\epsilon = vB dr = (r\omega B) dr$ (since $\vec{v} \perp \vec{B}$).

Integrating from $r=0$ to $r=L$:

$\epsilon = \int_{0}^{L} r\omega B dr = \omega B \int_{0}^{L} r dr = \omega B \left[ \frac{r^2}{2} \right]_{0}^{L} = \frac{1}{2} B \omega L^2$.

The potential at A is higher than at O.

The induced EMF across the rod OA is $\frac{1}{2} B \omega L^2$.