Question

The problem illustrates the electrostatic forces acting on a charge 'Q' placed at one corner of a square due to other charges at the remaining corners.

Answer 1

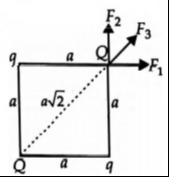
The forces F1, F2, and F3 are correctly depicted as the individual electrostatic forces exerted on the charge Q at the top-right corner by the charges q (top-left), q (bottom-right), and Q (bottom-left) respectively, assuming all charges have the same sign (repulsive interactions). The magnitudes are $F_1 = F_2 = k\frac{qQ}{a^2}$ and $F_3 = k\frac{Q^2}{2a^2}$.

Answer 2

Understanding the Setup

• Geometry: A square of side length 'a'.
• Charges:
  • Top-left corner: charge 'q'
  • Top-right corner: charge 'Q' (This is the charge on which we are analyzing the forces)
  • Bottom-right corner: charge 'q'
  • Bottom-left corner: charge 'Q'
• Assumption: All charges (q and Q) are of the same sign (e.g., all positive), leading to repulsive forces, as depicted by the outward-pointing force vectors.

Analysis of Forces on Charge Q (top-right corner)

According to Coulomb's Law, the force between two point charges is directly proportional to the product of their magnitudes and inversely proportional to the square of the distance between them. The principle of superposition states that the net force on a charge is the vector sum of all individual forces acting on it due to other charges.

Let $k = \frac{1}{4\pi\epsilon_0}$ be Coulomb's constant.

1. Force F1 (from charge 'q' at top-left corner):

   • Source: Charge 'q' at (top-left).
   • Distance: 'a' (along the top side).
   • Direction: Horizontally to the right, away from 'q' (repulsive).
   • Magnitude: $F_1 = k \frac{qQ}{a^2}$

2. Force F2 (from charge 'q' at bottom-right corner):

   • Source: Charge 'q' at (bottom-right).
   • Distance: 'a' (along the right side).
   • Direction: Vertically upwards, away from 'q' (repulsive).
   • Magnitude: $F_2 = k \frac{qQ}{a^2}$

3. Force F3 (from charge 'Q' at bottom-left corner):

   • Source: Charge 'Q' at (bottom-left).
   • Distance: The diagonal of the square, which is $a\sqrt{2}$.
   • Direction: Along the diagonal (at $45^\circ$ to the horizontal), upwards and to the right, away from the other 'Q' (repulsive).
   • Magnitude: $F_3 = k \frac{Q \cdot Q}{(a\sqrt{2})^2} = k \frac{Q^2}{2a^2}$

The diagram accurately represents the directions of these three individual forces acting on the charge 'Q' at the top-right corner, assuming all charges are of the same sign.

Net Force on Charge Q (top-right corner)

The net force ($\vec{F}_{net}$) on the charge 'Q' is the vector sum of $\vec{F_1}$, $\vec{F_2}$, and $\vec{F_3}$. We can decompose $\vec{F_3}$ into its horizontal (x) and vertical (y) components.

• $F_{3x} = F_3 \cos(45^\circ) = F_3 \frac{1}{\sqrt{2}}$
• $F_{3y} = F_3 \sin(45^\circ) = F_3 \frac{1}{\sqrt{2}}$

The components of the net force are:

• X-component: $F_{net,x} = F_1 + F_{3x} = \frac{kqQ}{a^2} + \frac{kQ^2}{2a^2} \frac{1}{\sqrt{2}}$
• Y-component: $F_{net,y} = F_2 + F_{3y} = \frac{kqQ}{a^2} + \frac{kQ^2}{2a^2} \frac{1}{\sqrt{2}}$

Thus, the net force vector is: $\vec{F}_{net} = \left( \frac{kqQ}{a^2} + \frac{kQ^2}{2\sqrt{2}a^2} \right) \hat{i} + \left( \frac{kqQ}{a^2} + \frac{kQ^2}{2\sqrt{2}a^2} \right) \hat{j}$ This can be simplified as: $\vec{F}_{net} = \frac{kQ}{a^2} \left( q + \frac{Q}{2\sqrt{2}} \right) (\hat{i} + \hat{j})$

The magnitude of the net force is: $|\vec{F}_{net}| = \sqrt{F_{net,x}^2 + F_{net,y}^2} = \sqrt{2 \left( \frac{kQ}{a^2} \left( q + \frac{Q}{2\sqrt{2}} \right) \right)^2}$ $|\vec{F}_{net}| = \sqrt{2} \frac{kQ}{a^2} \left( q + \frac{Q}{2\sqrt{2}} \right)$ $|\vec{F}_{net}| = \frac{kQ}{a^2} \left( q\sqrt{2} + \frac{Q}{2} \right)$ The direction of the net force is along the diagonal, at $45^\circ$ to the horizontal.

Conclusion

The provided diagram correctly illustrates the individual electrostatic forces (F1, F2, F3) acting on the charge 'Q' at the top-right corner of the square due to the other three charges, assuming all charges are of the same sign (repulsive forces).

---

The image depicts a square with charges at its corners and forces acting on the top-right charge 'Q'.

1. Force F1: Due to charge 'q' at the top-left corner. It is repulsive, acting horizontally right. Magnitude: $F_1 = k \frac{qQ}{a^2}$.
2. Force F2: Due to charge 'q' at the bottom-right corner. It is repulsive, acting vertically up. Magnitude: $F_2 = k \frac{qQ}{a^2}$.
3. Force F3: Due to charge 'Q' at the bottom-left corner. It is repulsive, acting diagonally up-right along the square's diagonal. Magnitude: $F_3 = k \frac{Q^2}{(a\sqrt{2})^2} = k \frac{Q^2}{2a^2}$.

The directions shown in the diagram are consistent with repulsive forces between like charges.

The net force on charge 'Q' is the vector sum of these three forces: $\vec{F}_{net} = \vec{F_1} + \vec{F_2} + \vec{F_3}$ $\vec{F}_{net} = \left( k \frac{qQ}{a^2} + k \frac{Q^2}{2a^2} \cos 45^\circ \right) \hat{i} + \left( k \frac{qQ}{a^2} + k \frac{Q^2}{2a^2} \sin 45^\circ \right) \hat{j}$ $\vec{F}_{net} = \left( k \frac{qQ}{a^2} + k \frac{Q^2}{2a^2} \frac{1}{\sqrt{2}} \right) \hat{i} + \left( k \frac{qQ}{a^2} + k \frac{Q^2}{2a^2} \frac{1}{\sqrt{2}} \right) \hat{j}$ $\vec{F}_{net} = \frac{kQ}{a^2} \left( q + \frac{Q}{2\sqrt{2}} \right) (\hat{i} + \hat{j})$

Magnitude of net force: $|\vec{F}_{net}| = \frac{kQ}{a^2} \left( q\sqrt{2} + \frac{Q}{2} \right)$.