Question

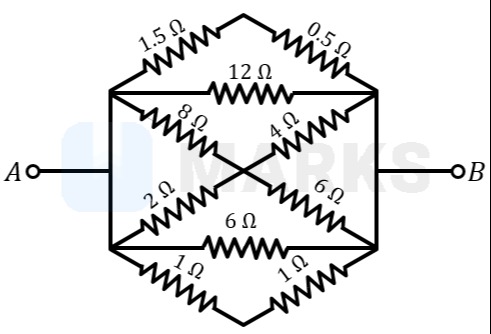
The problem asks for the equivalent resistance between points A and B of the given circuit. This is a complex network of resistors.

Answer 1

2.6577 \Omega

Answer 2

The given circuit is a complex network of resistors. We use nodal analysis to find the equivalent resistance between points A and B.

Let the potential at point A be $V_A = V$ and the potential at point B be $V_B = 0$. Let the potentials at the internal nodes be $V_C$ (top-left), $V_D$ (top-right), $V_E$ (bottom-left), and $V_F$ (bottom-right). The two $1 \, \Omega$ resistors at the bottom are in series, forming a $2 \, \Omega$ resistance between node E and node B.

Applying Kirchhoff's Current Law (KCL) at each node:

1. Node C: $\frac{V_C - V_A}{1.5} + \frac{V_C - V_D}{12} + \frac{V_C - V_E}{8} = 0$

   Multiplying by 24 (LCM of 1.5, 12, 8): $16(V_C - V_A) + 2(V_C - V_D) + 3(V_C - V_E) = 0$ $21V_C - 2V_D - 3V_E = 16V_A$ (Eq. 1)

2. Node D: $\frac{V_D - V_C}{12} + \frac{V_D - V_B}{0.5} + \frac{V_D - V_F}{4} = 0$

   Multiplying by 12 (LCM of 12, 0.5, 4): $(V_D - V_C) + 24(V_D - V_B) + 3(V_D - V_F) = 0$

   Since $V_B = 0$: $-V_C + 28V_D - 3V_F = 0$ (Eq. 2)

3. Node E: $\frac{V_E - V_A}{2} + \frac{V_E - V_C}{8} + \frac{V_E - V_F}{6} + \frac{V_E - V_B}{2} = 0$

   Multiplying by 24 (LCM of 2, 8, 6, 2): $12(V_E - V_A) + 3(V_E - V_C) + 4(V_E - V_F) + 12(V_E - V_B) = 0$

   Since $V_B = 0$: $-3V_C + 31V_E - 4V_F = 12V_A$ (Eq. 3)

4. Node F: $\frac{V_F - V_D}{4} + \frac{V_F - V_E}{6} + \frac{V_F - V_B}{1} = 0$

   Multiplying by 12 (LCM of 4, 6, 1): $3(V_F - V_D) + 2(V_F - V_E) + 12(V_F - V_B) = 0$

   Since $V_B = 0$: $-3V_D - 2V_E + 17V_F = 0$ (Eq. 4)

Let $V_A = 1 \, V$. We solve the system of linear equations for $V_C, V_D, V_E, V_F$.

From Eq. 2: $V_C = 28V_D - 3V_F$ From Eq. 4: $V_D = \frac{17V_F - 2V_E}{3}$

Substitute $V_C$ into Eq. 1: $21(28V_D - 3V_F) - 2V_D - 3V_E = 16$ $586V_D - 3V_E - 63V_F = 16$ (Eq. 5)

Substitute $V_D$ into Eq. 5: $586\left(\frac{17V_F - 2V_E}{3}\right) - 3V_E - 63V_F = 16$ $586(17V_F - 2V_E) - 9V_E - 189V_F = 48$ $9962V_F - 1172V_E - 9V_E - 189V_F = 48$ $-1181V_E + 9773V_F = 48$ (Eq. 6)

Substitute $V_C$ into Eq. 3: $-3(28V_D - 3V_F) + 31V_E - 4V_F = 12$ $-84V_D + 9V_F + 31V_E - 4V_F = 12$ $31V_E - 84V_D + 5V_F = 12$ (Eq. 7)

Substitute $V_D$ into Eq. 7: $31V_E - 84\left(\frac{17V_F - 2V_E}{3}\right) + 5V_F = 12$ $31V_E - 28(17V_F - 2V_E) + 5V_F = 12$ $31V_E - 476V_F + 56V_E + 5V_F = 12$ $87V_E - 471V_F = 12$ (Eq. 8)

Now we solve the system of Eq. 6 and Eq. 8 for $V_E$ and $V_F$: (Eq. 6) $-1181V_E + 9773V_F = 48$ (Eq. 8) $87V_E - 471V_F = 12$

From Eq. 8, divide by 3: $29V_E - 157V_F = 4 \implies V_E = \frac{4 + 157V_F}{29}$ Substitute $V_E$ into Eq. 6: $-1181\left(\frac{4 + 157V_F}{29}\right) + 9773V_F = 48$ $-4724 - 185497V_F + 283417V_F = 1392$ $97920V_F = 6116$ $V_F = \frac{6116}{97920} = \frac{1529}{24480}$

Substitute $V_F$ back into the expression for $V_E$: $V_E = \frac{4 + 157 \times \frac{1529}{24480}}{29} = \frac{4 + \frac{240073}{24480}}{29} = \frac{\frac{97920 + 240073}{24480}}{29} = \frac{337993}{24480 \times 29} = \frac{337993}{710000}$

Substitute $V_E$ and $V_F$ into the expression for $V_D$: $V_D = \frac{17V_F - 2V_E}{3} = \frac{17 \times \frac{1529}{24480} - 2 \times \frac{337993}{710000}}{3} = \frac{\frac{26093}{24480} - \frac{337993}{355000}}{3}$ $V_D = \frac{26093 \times 355000 - 337993 \times 24480}{3 \times 24480 \times 355000} = \frac{9263015000 - 8274023040}{26038800000} = \frac{988991960}{26038800000} = \frac{40357}{1065000}$

The total current $I_{AB}$ flowing from A to B is the sum of currents leaving A, or entering B. $I_{AB} = \frac{V_D - V_B}{0.5} + \frac{V_F - V_B}{1} + \frac{V_E - V_B}{2}$

Since $V_B = 0$: $I_{AB} = \frac{V_D}{0.5} + V_F + \frac{V_E}{2} = 2V_D + V_F + 0.5V_E$ $I_{AB} = 2 \times \frac{40357}{1065000} + \frac{1529}{24480} + 0.5 \times \frac{337993}{710000}$

Converting to decimals for approximation: $V_D \approx 0.0378938967$ $V_F \approx 0.0624599673$ $V_E \approx 0.4760464789$

$I_{AB} \approx 2(0.0378938967) + 0.0624599673 + 0.5(0.4760464789)$ $I_{AB} \approx 0.0757877934 + 0.0624599673 + 0.23802323945$ $I_{AB} \approx 0.376270999$

The equivalent resistance $R_{eq} = \frac{V_A}{I_{AB}} = \frac{1}{0.376270999} \approx 2.6577 \, \Omega$.