Question

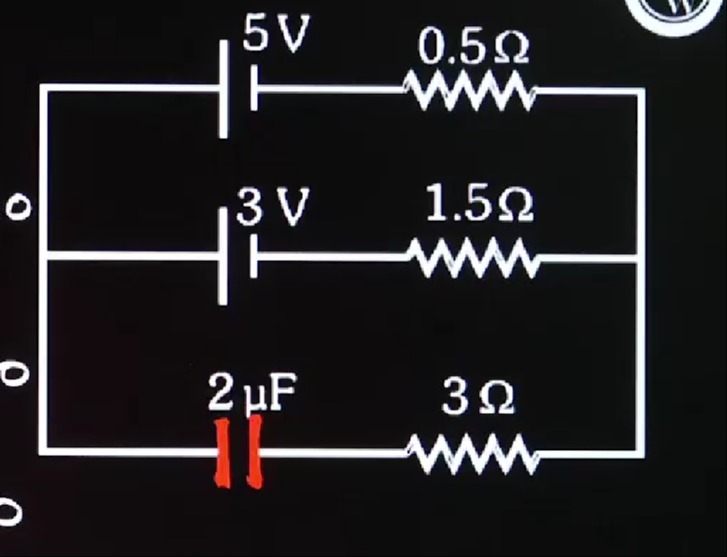
5 V 0.5$\Omega$ 3 V 1.5$\Omega$ 2 $\mu$F 3$\Omega$

• A. The charge on the capacitor is 9 $\mu$C.
• B. The charge on the capacitor is -9 $\mu$C.
• C. The voltage across the capacitor is 4.5 V.
• D. The voltage across the capacitor is -4.5 V.

Answer 1

Answer: (A)

The charge on the capacitor is 9 $\mu$C.

Answer 2

In a steady-state DC circuit, a capacitor acts as an open circuit, meaning no current flows through its branch. Let $V_A$ and $V_B$ be the potentials of the common nodes.

For the first branch: $V_A - V_B = -5\text{ V} + 0.5 I_1$, where $I_1$ is the current from A to B. For the second branch: $V_A - V_B = -3\text{ V} + 1.5 I_2$, where $I_2$ is the current from A to B. For the third branch (capacitor): In steady state, the current $I_3 = 0$. The voltage across the capacitor is $V_C = V_A - V_B$.

By KCL at node A: $I_1 + I_2 + I_3 = 0$. Since $I_3 = 0$, $I_1 + I_2 = 0$, which means $I_2 = -I_1$.

Substituting $I_2 = -I_1$ into the second branch equation: $V_A - V_B = -3\text{ V} + 1.5 (-I_1) = -3\text{ V} - 1.5 I_1$.

Equating the expressions for $V_A - V_B$: $-5 + 0.5 I_1 = -3 - 1.5 I_1$ $2 I_1 = 2$ $I_1 = 1$ A.

Now, calculate $V_A - V_B$: $V_A - V_B = -5 + 0.5(1) = -4.5$ V.

The voltage across the capacitor is $V_C = V_A - V_B = -4.5$ V. The charge on the capacitor is $Q = C V_C$. $C = 2 \mu$F $= 2 \times 10^{-6}$ F. $Q = (2 \times 10^{-6} \text{ F}) \times (-4.5 \text{ V}) = -9 \times 10^{-6}$ C $= -9 \mu$C.

The negative sign indicates the polarity of the charge. The magnitude of the charge on the capacitor is $9 \mu$C.