Question

To find the node voltages V1, V2, and V3, we will use Kirchhoff's Current Law (KCL) at each node. We will assume the currents leaving a node are positive. The ground node is at 0 V.

Circuit Parameters:

• Resistors:
  • R12 (between V1 and V2) = 46 Ω
  • R23 (between V2 and V3) = 46 Ω
  • R1g (between V1 and ground) = 3 Ω
  • R2g (between V2 and ground) = 46 Ω
  • R3g (between V3 and ground) = 3 Ω
  • R13 (between V1 and V3) = 6 Ω
• Current Sources:
  • I1 (entering V1) = 9.75 A
  • I2 (entering V3) = 1.75 A

KCL at Node V1:

The sum of currents leaving V1 is zero. Currents from the current source are entering, so they are negative when considering leaving currents as positive. $\frac{V_1 - V_2}{46} + \frac{V_1 - 0}{3} + \frac{V_1 - V_3}{6} - 9.75 = 0$

To clear denominators, multiply by the LCM of 46, 3, 6 which is 138: $3(V_1 - V_2) + 46V_1 + 23(V_1 - V_3) - 9.75 \times 138 = 0$ $3V_1 - 3V_2 + 46V_1 + 23V_1 - 23V_3 - 1345.5 = 0$ $(3 + 46 + 23)V_1 - 3V_2 - 23V_3 = 1345.5$ $72V_1 - 3V_2 - 23V_3 = 1345.5 \quad (1)$

KCL at Node V2:

$\frac{V_2 - V_1}{46} + \frac{V_2 - V_3}{46} + \frac{V_2 - 0}{46} = 0$

Multiply by 46: $V_2 - V_1 + V_2 - V_3 + V_2 = 0$ $-V_1 + 3V_2 - V_3 = 0 \quad (2)$

KCL at Node V3:

$\frac{V_3 - V_2}{46} + \frac{V_3 - 0}{3} + \frac{V_3 - V_1}{6} - 1.75 = 0$

To clear denominators, multiply by 138: $3(V_3 - V_2) + 46V_3 + 23(V_3 - V_1) - 1.75 \times 138 = 0$ $3V_3 - 3V_2 + 46V_3 + 23V_3 - 23V_1 - 241.5 = 0$ $-23V_1 - 3V_2 + (3 + 46 + 23)V_3 = 241.5$ $-23V_1 - 3V_2 + 72V_3 = 241.5 \quad (3)$

Now we have a system of three linear equations:

1. $72V_1 - 3V_2 - 23V_3 = 1345.5$
2. $-V_1 + 3V_2 - V_3 = 0$
3. $-23V_1 - 3V_2 + 72V_3 = 241.5$

From Equation (2), we can express $V_2$ in terms of $V_1$ and $V_3$: $3V_2 = V_1 + V_3$ $V_2 = \frac{V_1 + V_3}{3} \quad (4)$

Substitute Equation (4) into Equation (1): $72V_1 - 3\left(\frac{V_1 + V_3}{3}\right) - 23V_3 = 1345.5$ $72V_1 - (V_1 + V_3) - 23V_3 = 1345.5$ $72V_1 - V_1 - V_3 - 23V_3 = 1345.5$ $71V_1 - 24V_3 = 1345.5 \quad (5)$

Substitute Equation (4) into Equation (3): $-23V_1 - 3\left(\frac{V_1 + V_3}{3}\right) + 72V_3 = 241.5$ $-23V_1 - (V_1 + V_3) + 72V_3 = 241.5$ $-23V_1 - V_1 - V_3 + 72V_3 = 241.5$ $-24V_1 + 71V_3 = 241.5 \quad (6)$

Now we have a system of two linear equations with two unknowns ($V_1$, $V_3$): 5. $71V_1 - 24V_3 = 1345.5$ 6. $-24V_1 + 71V_3 = 241.5$

Multiply Equation (5) by 71 and Equation (6) by 24 to eliminate $V_3$: $71 \times (71V_1 - 24V_3) = 71 \times 1345.5 \implies 5041V_1 - 1704V_3 = 95530.5$ $24 \times (-24V_1 + 71V_3) = 24 \times 241.5 \implies -576V_1 + 1704V_3 = 5796$

Add the two new equations: $(5041 - 576)V_1 + (-1704 + 1704)V_3 = 95530.5 + 5796$ $4465V_1 = 101326.5$ $V_1 = \frac{101326.5}{4465} = 22.695$ V

Now, substitute $V_1 = 22.695$ into Equation (6): $-24(22.695) + 71V_3 = 241.5$ $-544.68 + 71V_3 = 241.5$ $71V_3 = 241.5 + 544.68$ $71V_3 = 786.18$ $V_3 = \frac{786.18}{71} = 11.073$ V (approx)

Alternatively, using the determinant method for V3: Multiply Equation (5) by 24 and Equation (6) by 71 to eliminate $V_1$: $24 \times (71V_1 - 24V_3) = 24 \times 1345.5 \implies 1704V_1 - 576V_3 = 32292$ $71 \times (-24V_1 + 71V_3) = 71 \times 241.5 \implies -1704V_1 + 5041V_3 = 17146.5$

Add the two new equations: $(1704 - 1704)V_1 + (-576 + 5041)V_3 = 32292 + 17146.5$ $4465V_3 = 49438.5$ $V_3 = \frac{49438.5}{4465} = 11.0725$ V

Finally, calculate $V_2$ using Equation (4): $V_2 = \frac{V_1 + V_3}{3} = \frac{22.695 + 11.0725}{3} = \frac{33.7675}{3} = 11.255833...$ V

Answer 1

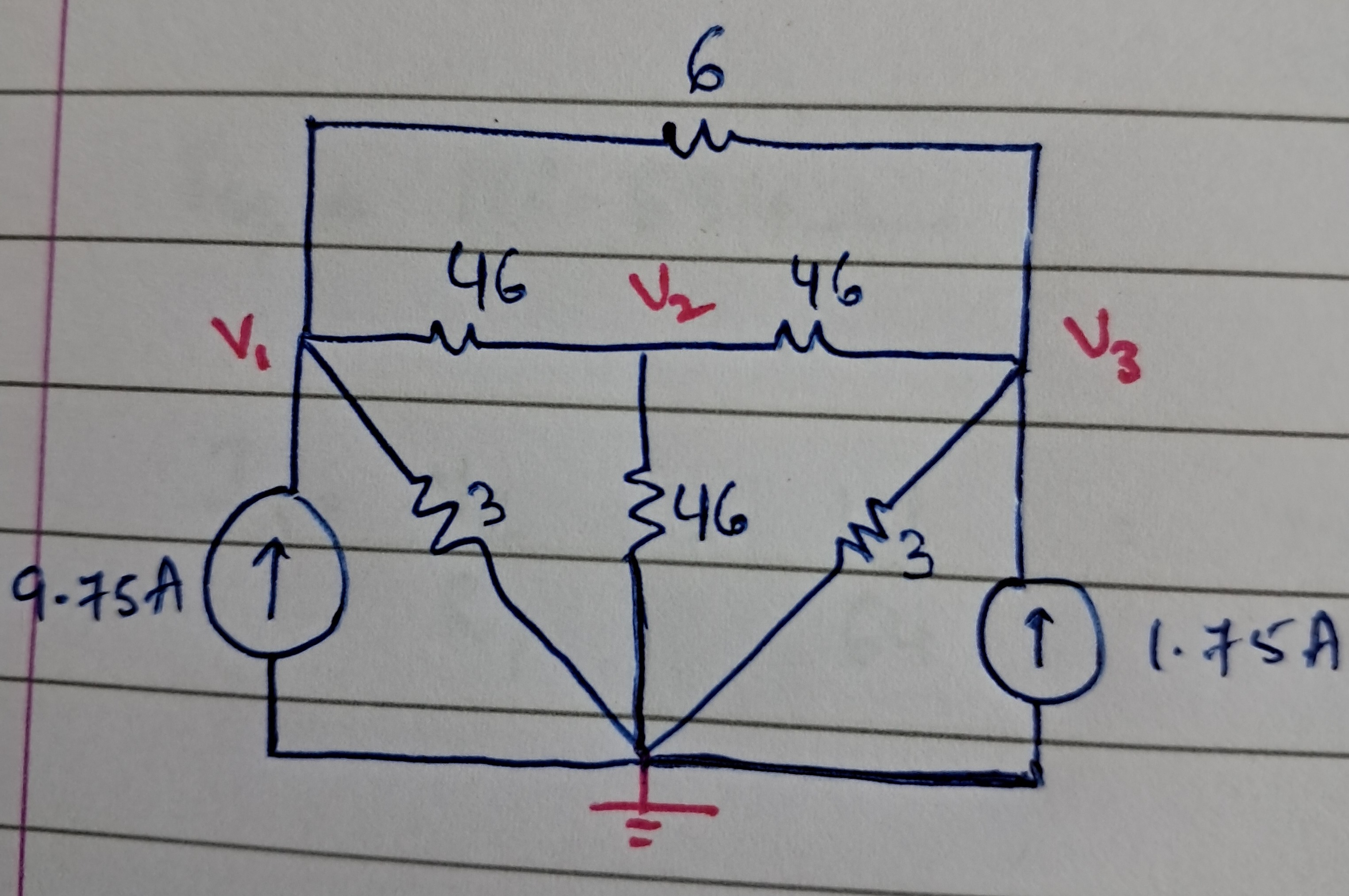
V1 = 22.695V, V2 = 11.256V, V3 = 11.073V

Answer 2

The node voltages are calculated using Kirchhoff's Current Law (KCL) at each node. The KCL equations are then solved to find the values of V1, V2, and V3.