Question
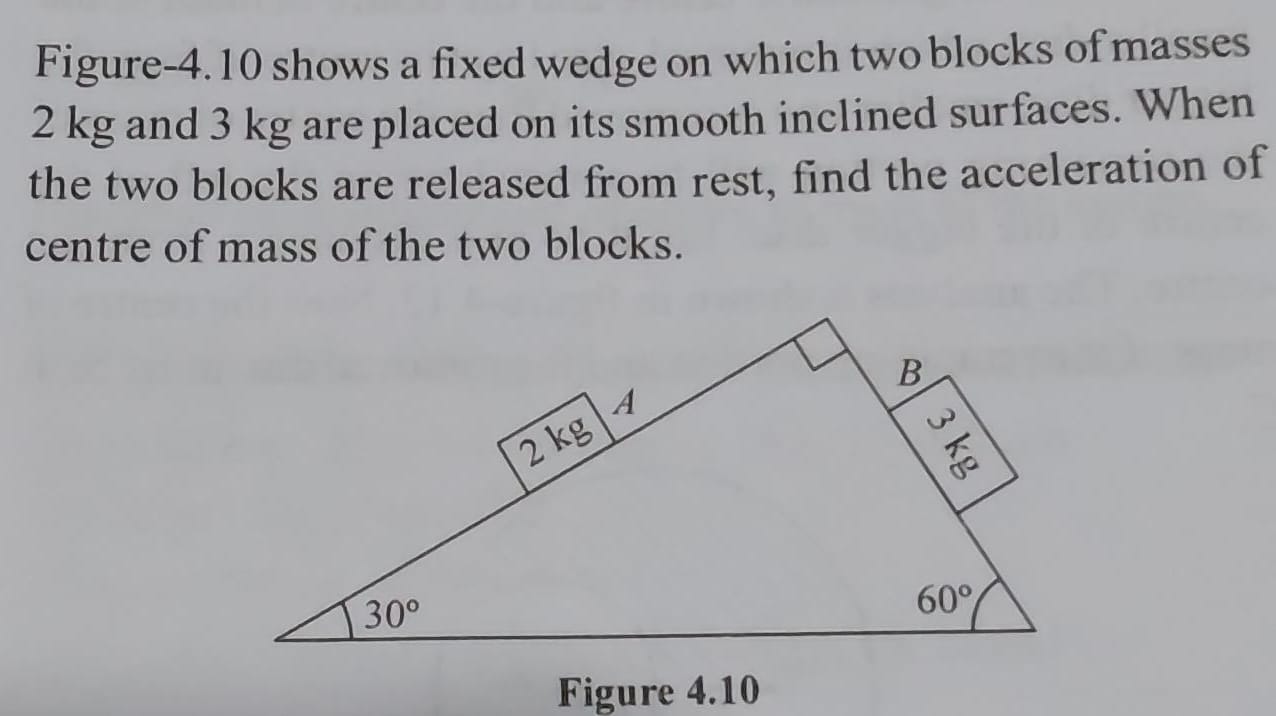
Question: Figure-4.10 shows a fixed wedge on which two blocks of masses 2 kg and 3 kg are placed on its smooth...
Figure-4.10 shows a fixed wedge on which two blocks of masses 2 kg and 3 kg are placed on its smooth inclined surfaces. When the two blocks are released from rest, find the acceleration of centre of mass of the two blocks.
Answer
The acceleration of the center of mass of the two blocks is 107g.
Explanation
Solution
- Calculate individual accelerations down the smooth inclines: a1=gsin(30∘)=g/2 and a2=gsin(60∘)=3g/2.
- Define a horizontal (x) and vertical (y) coordinate system. Assume inclines slope downwards to the right, so acceleration vectors are at angles −30∘ and −60∘ with the horizontal.
- Express accelerations as vectors: a1=2g(cos(−30∘)i^+sin(−30∘)j^) and a2=23g(cos(−60∘)i^+sin(−60∘)j^).
- Calculate the acceleration of the center of mass using aCM=m1+m2m1a1+m2a2.
- Compute the magnitude of aCM.
