Question

Find ⅰ) acd", when v = 30ms$^{-1}$

ⅱ) acd" at x = 15 m

Answer 1

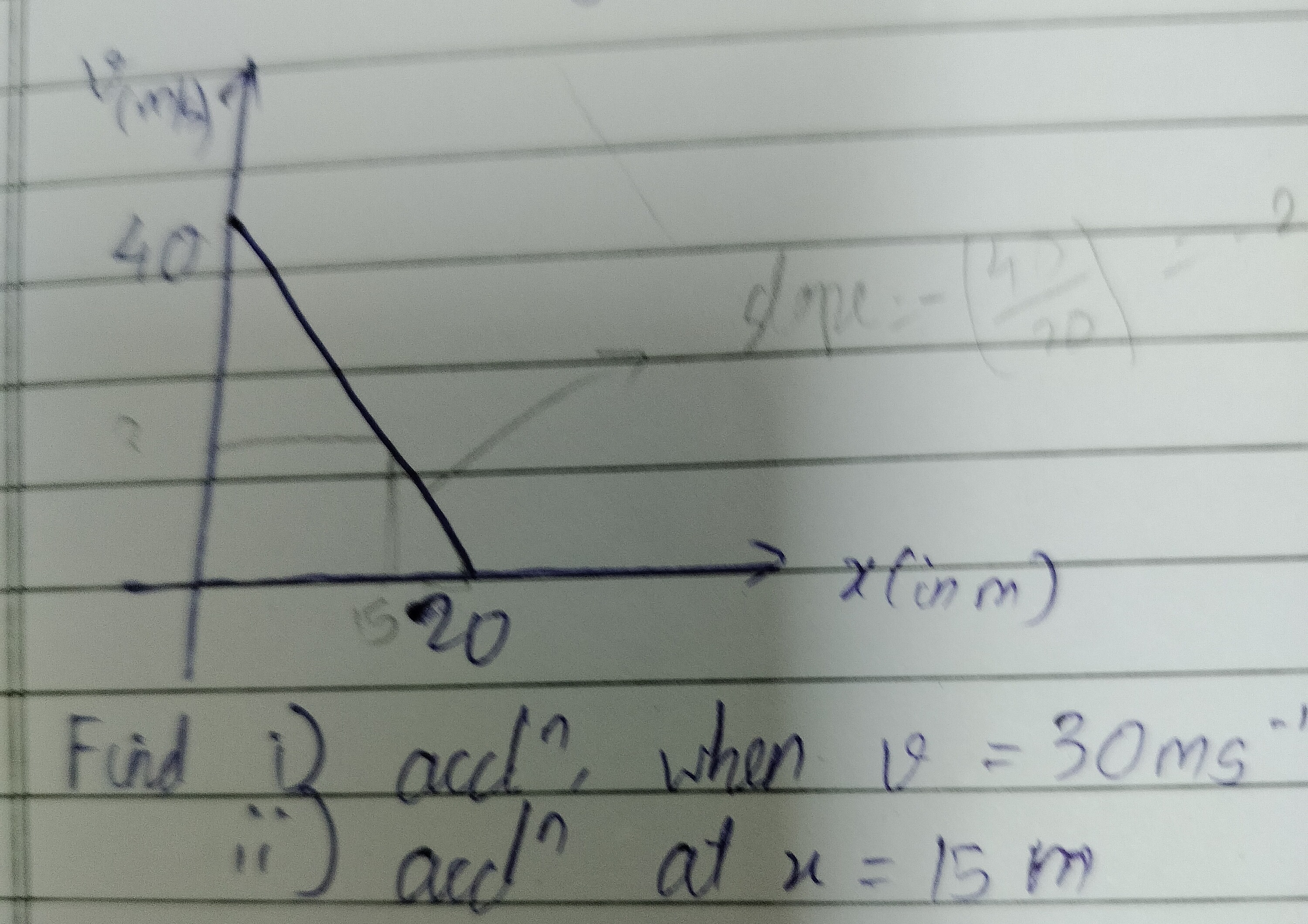
-1 ms$^{-2}$ for i) and -1 ms$^{-2}$ for ii)

Answer 2

The graph shows the relationship between $v^2$ and $x$. The graph is a straight line passing through the points $(x_1, v_1^2) = (0, 40)$ and $(x_2, v_2^2) = (20, 0)$.

The equation of the straight line is given by $v^2 - v_1^2 = \frac{v_2^2 - v_1^2}{x_2 - x_1} (x - x_1)$. Substituting the given points, we get: $v^2 - 40 = \frac{0 - 40}{20 - 0} (x - 0)$ $v^2 - 40 = \frac{-40}{20} x$ $v^2 - 40 = -2x$ $v^2 = -2x + 40$

The acceleration $a$ is related to velocity $v$ and position $x$ by the formula $a = v \frac{dv}{dx}$. We can find $\frac{dv}{dx}$ by differentiating the equation $v^2 = -2x + 40$ with respect to to $x$. Differentiating both sides with respect to $x$: $\frac{d}{dx}(v^2) = \frac{d}{dx}(-2x + 40)$ Using the chain rule on the left side, $\frac{d}{dx}(v^2) = \frac{d(v^2)}{dv} \frac{dv}{dx} = 2v \frac{dv}{dx}$. So, $2v \frac{dv}{dx} = -2$. Dividing by 2, we get $v \frac{dv}{dx} = -1$. Since $a = v \frac{dv}{dx}$, the acceleration is $a = -1 \, \text{ms}^{-2}$.

The acceleration is constant and equal to $-1 \, \text{ms}^{-2}$ for the motion described by the equation $v^2 = -2x + 40$.

ⅰ) Find acceleration when $v = 30 \, \text{ms}^{-1}$. Since the acceleration is constant, its value is $-1 \, \text{ms}^{-2}$ at any velocity for which the relationship $v^2 = -2x + 40$ holds. While the graph shows the velocity decreasing from $\sqrt{40} \approx 6.32 \, \text{ms}^{-1}$ to $0 \, \text{ms}^{-1}$, if we assume the relationship holds even for $v=30 \, \text{ms}^{-1}$, the acceleration is still the constant value we calculated. Acceleration when $v = 30 \, \text{ms}^{-1}$ is $-1 \, \text{ms}^{-2}$.

ⅱ) Find acceleration at $x = 15 \, \text{m}$. Since the acceleration is constant, its value at $x = 15 \, \text{m}$ is $-1 \, \text{ms}^{-2}$. We can also find the velocity at $x = 15 \, \text{m}$: $v^2 = -2(15) + 40 = -30 + 40 = 10$. $v = \sqrt{10} \, \text{ms}^{-1}$. The acceleration at this position is $-1 \, \text{ms}^{-2}$.

Explanation of the solution: The given graph is of $v^2$ versus $x$. The graph is a straight line, indicating a linear relationship between $v^2$ and $x$. The equation of the line is found to be $v^2 = -2x + 40$. The acceleration $a$ is related to $v$ and $x$ by $a = v \frac{dv}{dx}$. Differentiating the equation $v^2 = -2x + 40$ with respect to $x$, we get $2v \frac{dv}{dx} = -2$, which simplifies to $v \frac{dv}{dx} = -1$. Thus, the acceleration $a = -1 \, \text{ms}^{-2}$. Since the acceleration is a constant value, it is the same at any given velocity or position within the motion described by the relationship.