Question

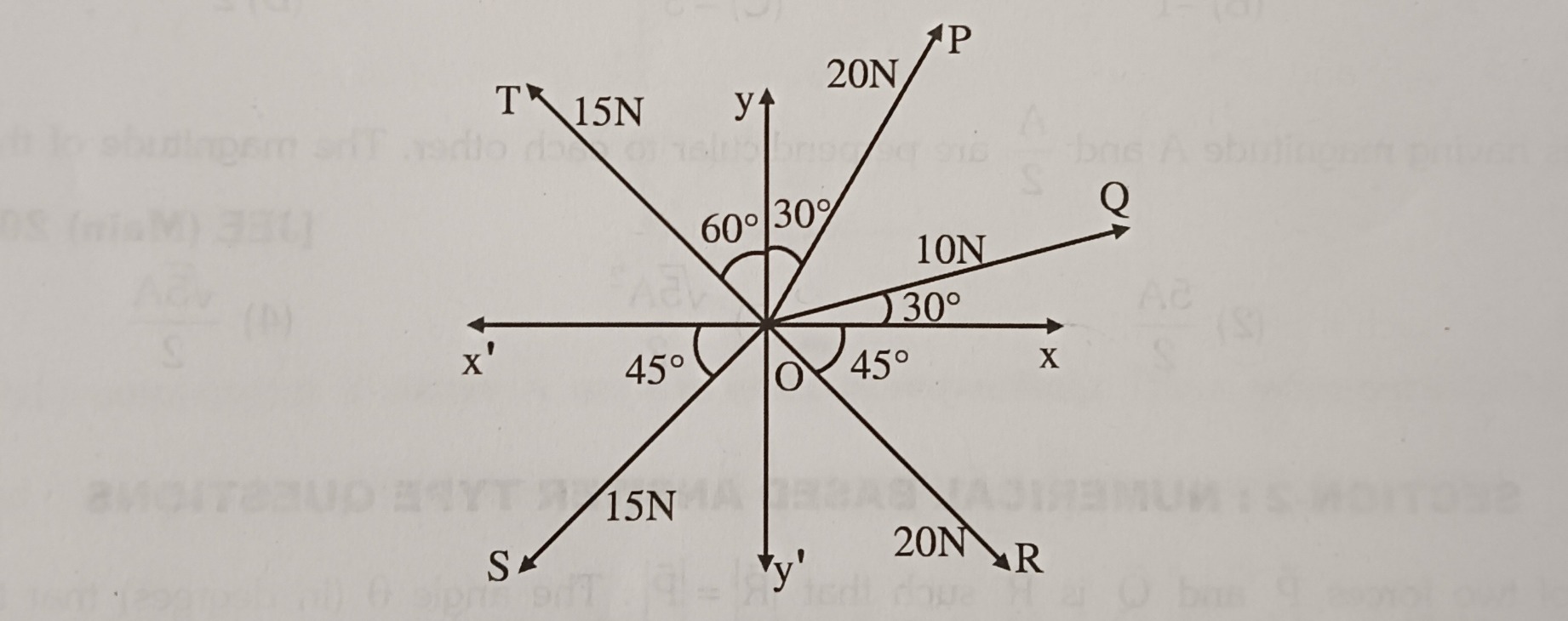
To find the resultant force, we resolve each force into its x and y components and then sum them up. Let the positive x-axis be along 'x' and the positive y-axis be along 'y'. Angles are measured counter-clockwise from the positive x-axis.

1. Force Q (10 N): Angle with +x-axis = $30^\circ$. $Q_x = 10 \cos 30^\circ = 10 \left(\frac{\sqrt{3}}{2}\right) = 5\sqrt{3}$ N $Q_y = 10 \sin 30^\circ = 10 \left(\frac{1}{2}\right) = 5$ N

2. Force P (20 N): Angle with +y-axis = $30^\circ$. So, angle with +x-axis = $90^\circ - 30^\circ = 60^\circ$. $P_x = 20 \cos 60^\circ = 20 \left(\frac{1}{2}\right) = 10$ N $P_y = 20 \sin 60^\circ = 20 \left(\frac{\sqrt{3}}{2}\right) = 10\sqrt{3}$ N

3. Force T (15 N): Angle with -x-axis ($x'$) = $60^\circ$. So, angle with +x-axis = $180^\circ - 60^\circ = 120^\circ$. $T_x = 15 \cos 120^\circ = 15 \left(-\frac{1}{2}\right) = -7.5$ N $T_y = 15 \sin 120^\circ = 15 \left(\frac{\sqrt{3}}{2}\right) = 7.5\sqrt{3}$ N

4. Force S (15 N): Angle with -x-axis ($x'$) = $45^\circ$ (in the third quadrant). So, angle with +x-axis = $180^\circ + 45^\circ = 225^\circ$. $S_x = 15 \cos 225^\circ = 15 \left(-\frac{1}{\sqrt{2}}\right) = -\frac{15}{\sqrt{2}}$ N $S_y = 15 \sin 225^\circ = 15 \left(-\frac{1}{\sqrt{2}}\right) = -\frac{15}{\sqrt{2}}$ N

5. Force R (20 N): Angle with +x-axis = $45^\circ$ (in the fourth quadrant). So, angle with +x-axis = $360^\circ - 45^\circ = 315^\circ$. $R_x = 20 \cos 315^\circ = 20 \left(\frac{1}{\sqrt{2}}\right) = \frac{20}{\sqrt{2}}$ N $R_y = 20 \sin 315^\circ = 20 \left(-\frac{1}{\sqrt{2}}\right) = -\frac{20}{\sqrt{2}}$ N

Now, sum the x-components to find $F_x$: $F_x = Q_x + P_x + T_x + S_x + R_x$ $F_x = 5\sqrt{3} + 10 - 7.5 - \frac{15}{\sqrt{2}} + \frac{20}{\sqrt{2}}$ $F_x = (10 - 7.5) + 5\sqrt{3} + \left(\frac{20 - 15}{\sqrt{2}}\right)$ $F_x = 2.5 + 5\sqrt{3} + \frac{5}{\sqrt{2}}$ $F_x = 2.5 + 5\sqrt{3} + \frac{5\sqrt{2}}{2}$ N

Now, sum the y-components to find $F_y$: $F_y = Q_y + P_y + T_y + S_y + R_y$ $F_y = 5 + 10\sqrt{3} + 7.5\sqrt{3} - \frac{15}{\sqrt{2}} - \frac{20}{\sqrt{2}}$ $F_y = 5 + (10 + 7.5)\sqrt{3} - \left(\frac{15 + 20}{\sqrt{2}}\right)$ $F_y = 5 + 17.5\sqrt{3} - \frac{35}{\sqrt{2}}$ $F_y = 5 + 17.5\sqrt{3} - \frac{35\sqrt{2}}{2}$ N

The resultant force is $\vec{F_R} = F_x \hat{i} + F_y \hat{j}$. The magnitude of the resultant force is $F_R = \sqrt{F_x^2 + F_y^2}$.

Substituting the approximate values: $\sqrt{2} \approx 1.414$, $\sqrt{3} \approx 1.732$ $F_x = 2.5 + 5(1.732) + 2.5(1.414) = 2.5 + 8.66 + 3.535 = 14.695$ N $F_y = 5 + 17.5(1.732) - 17.5(1.414) = 5 + 30.31 - 24.745 = 5 + 5.565 = 10.565$ N

$F_R = \sqrt{(14.695)^2 + (10.565)^2} = \sqrt{216.09 + 111.62} = \sqrt{327.71} \approx 18.10$ N

Answer 1

No options are provided in the question. The calculated resultant force components are $F_x = 2.5 + 5\sqrt{3} + \frac{5\sqrt{2}}{2} \text{ N and } F_y = 5 + 17.5\sqrt{3} - \frac{35\sqrt{2}}{2} \text{ N}$. The magnitude is approximately $18.10 \text{ N}$.

Answer 2

The problem requires finding the resultant force of multiple forces acting at a point. This is achieved by:

1. Identifying each force's magnitude and its angle with respect to a common reference axis (usually the positive x-axis).
2. Resolving each force into its perpendicular components along the x-axis and y-axis using trigonometry ($F_x = F \cos\theta$, $F_y = F \sin\theta$).
3. Summing all x-components to get the net x-component ($F_x = \sum F_{ix}$).
4. Summing all y-components to get the net y-component ($F_y = \sum F_{iy}$).
5. Calculating the magnitude of the resultant force using the Pythagorean theorem ($F_R = \sqrt{F_x^2 + F_y^2}$).