Question

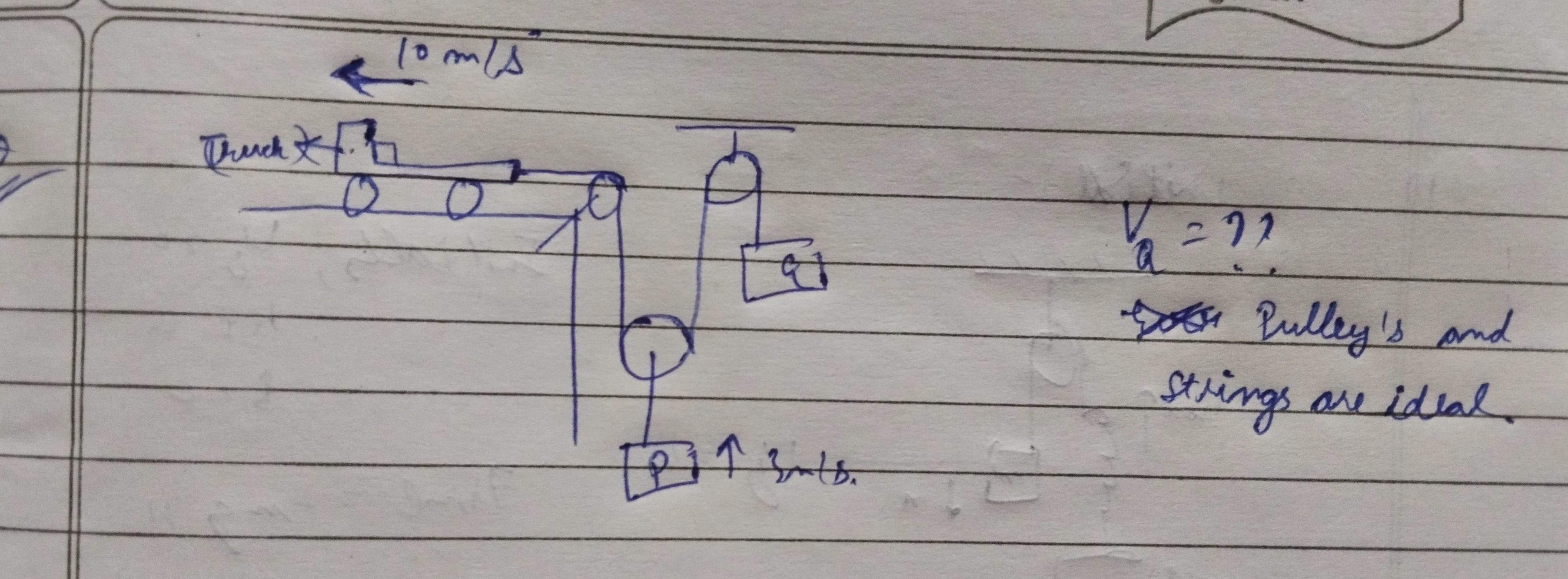
To solve this problem, we need to analyze the velocities using the principle of inextensibility of strings and the properties of ideal pulleys. We will consider two main parts of the system:

1. The system involving the truck, Pulley 1 (fixed), and Pulley 2 (movable), which determines the velocity of Block P.
2. The system involving Pulley 2, Pulley 3 (fixed), and Block Q.

Let's establish a coordinate system: upward direction as positive for vertical velocities, and leftward direction as positive for horizontal velocities.

Part 1: Truck, Pulley 1, and Pulley 2 (and Block P)

• Given:

  • Velocity of the truck v_truck = 10 m/s (leftward).
  • Velocity of Block P v_P = 3 m/s (upward).

• Analysis of Pulley 2: Pulley 2 is a movable pulley. One end of the string (let's call it S_ceiling) is attached to the ceiling, so its velocity v_S_ceiling = 0. The other end of the string (let's call it S_from_P1) comes from Pulley 1. Block P is attached to the axle of Pulley 2, so the velocity of Pulley 2 is v_P2 = v_P = 3 m/s (upward). For a movable pulley, the velocity of the pulley's center is the average of the velocities of the two string segments passing over it: v_P2 = (v_S_ceiling + v_S_from_P1) / 2 3 m/s = (0 + v_S_from_P1) / 2 Therefore, v_S_from_P1 = 6 m/s (upward). This is the velocity of the string segment that leaves Pulley 1 downwards.

• Analysis of Pulley 1 (and the truck): Pulley 1 is a fixed pulley. The string from the truck goes over Pulley 1 and then vertically downwards. The speed of the string must be constant throughout its length. Let v_string_speed be the speed of the string. The string segment leaving Pulley 1 downwards has a speed of v_S_from_P1 = 6 m/s. So, v_string_speed = 6 m/s. Now, consider the truck. The diagram shows the truck on a horizontal surface, and the fixed pulley (Pulley 1) is likely above the truck's level. Let x be the horizontal distance of the truck from the vertical line passing through Pulley 1, and h be the vertical distance of Pulley 1 above the truck's level. The length of the string segment from the truck to Pulley 1 is L_truck = sqrt(x^2 + h^2). The rate of change of this length is dL_truck/dt = (x / sqrt(x^2 + h^2)) * dx/dt. The term x / sqrt(x^2 + h^2) is cos(theta), where theta is the angle the string makes with the horizontal at the truck. So, dL_truck/dt = cos(theta) * v_truck_x. The speed at which the string is being pulled by the truck is v_string_speed = -dL_truck/dt = -cos(theta) * v_truck_x. Since v_truck = 10 m/s to the left, v_truck_x = 10 m/s (if we take left as positive x). So, 6 m/s = cos(theta) * 10 m/s. cos(theta) = 6/10 = 3/5. This confirms that the string from the truck is not horizontal; it's inclined, which is consistent with the diagram showing Pulley 1 above the truck. This also confirms our calculated v_S_from_P1 = 6 m/s is consistent with the truck's speed.

Part 2: Pulley 2, Pulley 3, and Block Q

• Given:
  • Velocity of Pulley 2 (and Block P) v_P2 = v_P = 3 m/s (upward).
• Analysis of Pulley 3: Pulley 3 is a fixed pulley. One end of the string is attached to Pulley 2, and the other end is attached to Block Q. For a fixed pulley, the speeds of the string segments on both sides are equal. The velocity of the string segment attached to Pulley 2 is v_P2 = 3 m/s (upward). Let y_Q be the position of Block Q and y_P2 be the position of Pulley 2. Let H_P3 be the fixed height of Pulley 3. The total length of the string L_string2 passing over Pulley 3 is L_string2 = (H_P3 - y_P2) + (H_P3 - y_Q). Differentiating with respect to time: dL_string2/dt = -dy_P2/dt - dy_Q/dt = 0. v_P2_y + v_Q_y = 0. So, v_Q_y = -v_P2_y. Since v_P2_y = 3 m/s (upward), v_Q_y = -3 m/s. This means Block Q is moving downwards with a speed of 3 m/s.

Answer 1

3 m/s downwards

Answer 2

1. Pulley 2 analysis: Block P is attached to a movable pulley (Pulley 2). One end of the string over Pulley 2 is fixed to the ceiling (velocity = 0). The other end of the string comes from Pulley 1. The velocity of the movable pulley is the average of the velocities of the two string ends. Given v_P = 3 m/s upwards, the string segment coming from Pulley 1 must be moving upwards at 2 * 3 m/s = 6 m/s.
2. Pulley 1 and Truck analysis: The string from the truck goes over a fixed pulley (Pulley 1). The speed of the string is uniform. Since the string segment leaving Pulley 1 downwards moves at 6 m/s upwards, the string is being pulled into Pulley 1 at 6 m/s. If the truck moves at 10 m/s horizontally, this implies the string from the truck to Pulley 1 is not horizontal; it's inclined such that the component of the truck's velocity along the string is 6 m/s (10 * cos(theta) = 6, so cos(theta) = 3/5). This consistency check confirms the string speed is 6 m/s.
3. Pulley 3 analysis: Pulley 3 is a fixed pulley. One end of the string is attached to Pulley 2 (moving at 3 m/s upwards). The other end is attached to Block Q. For a fixed pulley, the velocity components along the string are equal in magnitude and opposite in direction for the two hanging parts. If Pulley 2 moves up at 3 m/s, Block Q must move down at 3 m/s to keep the string length constant.