Question
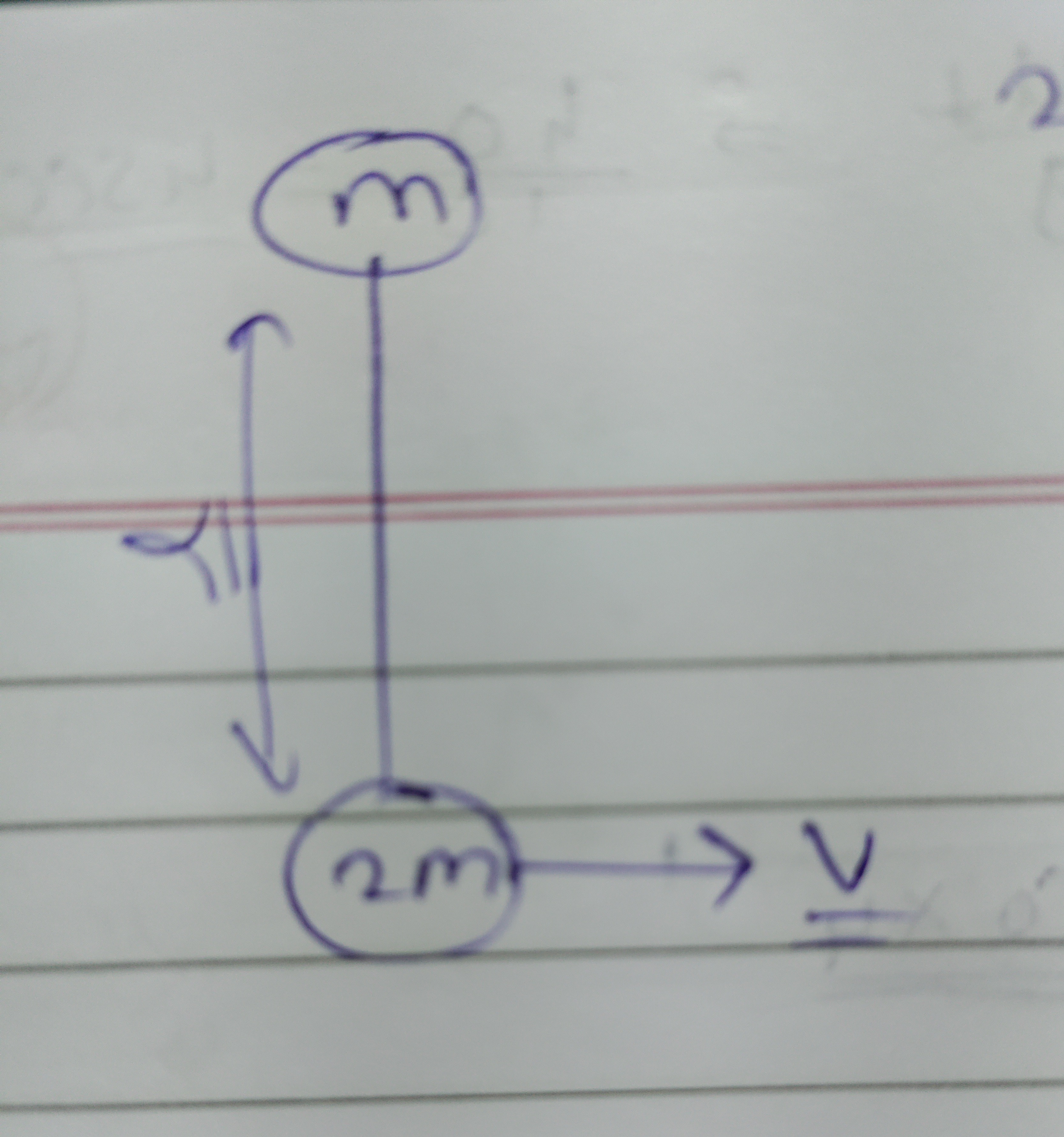
Question: The problem describes a rigid rod connecting two masses, 'm' and '2m', with a length 'l'. The mass '...
The problem describes a rigid rod connecting two masses, 'm' and '2m', with a length 'l'. The mass '2m' is given an instantaneous horizontal velocity 'v'. We need to find the angular velocity of the system immediately after this impulse.
Answer
The angular velocity of the system is lv.
Explanation
Solution
The system's motion is a combination of translation and rotation. We first find the velocity of the center of mass using the impulse-momentum theorem. Then, using the rigid body velocity formula (VP=VCM+ω×rP/CM) applied to the mass '2m', whose velocity is known, we solve for the angular velocity ω. Alternatively, recognizing that the mass 'm' comes to instantaneous rest, it acts as the instantaneous center of rotation, simplifying the calculation of ω.
