Question

The problem presents a complex circuit diagram with multiple voltage sources and resistors, along with nine numbered nodes. The goal is to determine the potential at each of these numbered nodes.

Answer 1

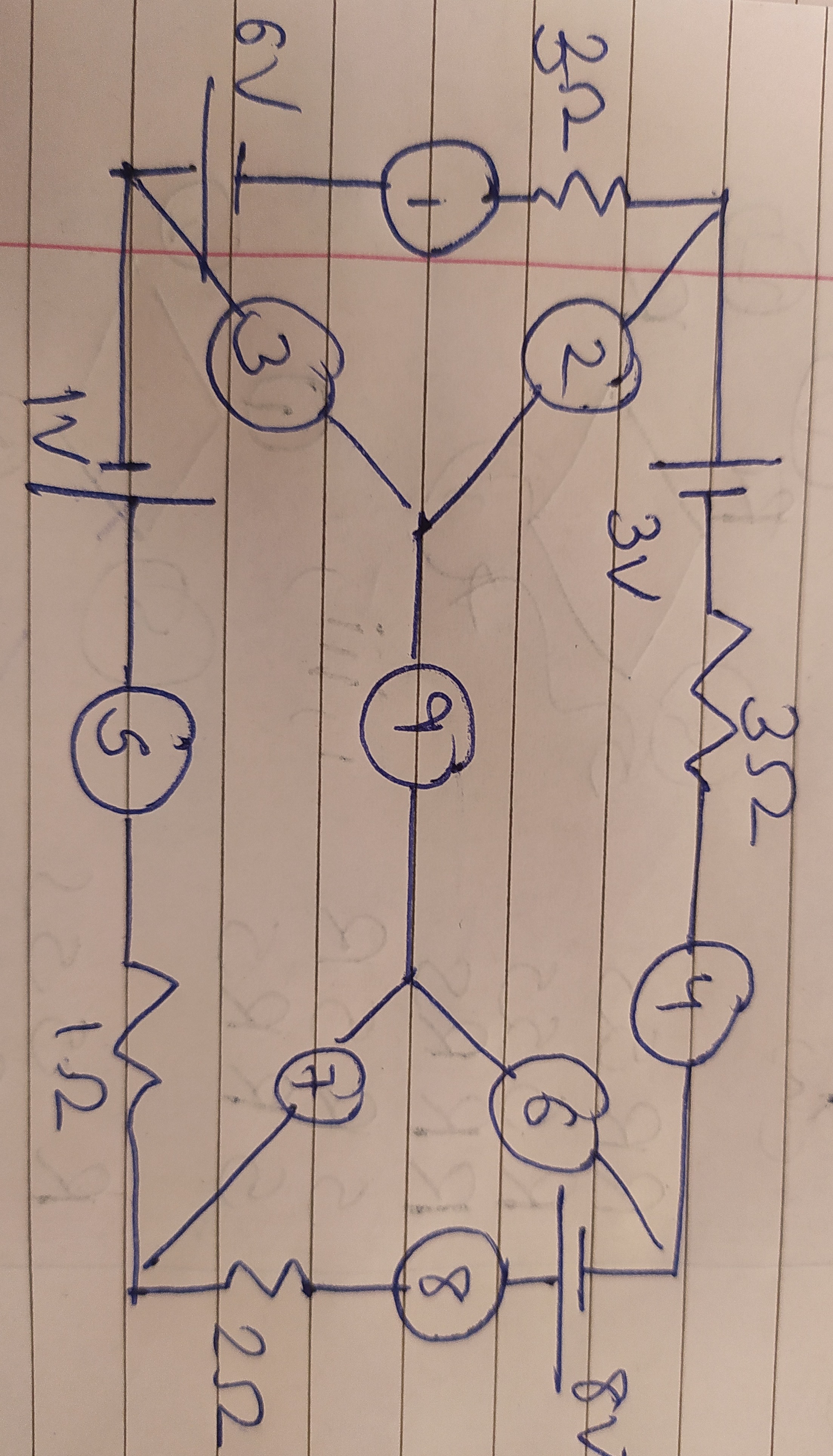
V1=2V, V2=8V, V3=8V, V4=5V, V5=9V, V6=8V, V7=8V, V8=0V, V9=8V

Answer 2

The solution uses Nodal Analysis to determine the potential at each node in the circuit. Here's a breakdown of the steps:

1. Choose a Reference Node: Node 8 is chosen as the reference node (ground) and assigned a potential of 0V, i.e., $V_8 = 0V$.

2. Determine Potentials of Directly Connected Nodes:

   • Node 6: Since an 8V voltage source is connected between Node 8 (negative terminal) and Node 6 (positive terminal), $V_6 = 8V$.

3. Interpret the Central Connections: The diagram shows direct wire connections from the central Node 9 to Nodes 2, 3, 6, and 7. This implies that all these nodes are at the same electrical potential. Therefore: $V_9 = V_2 = V_3 = V_6 = V_7 = 8V$.

4. Determine Remaining Node Potentials using Voltage Sources:

   • Node 4: A 3V voltage source is connected between Node 4 (negative terminal) and Node 2 (positive terminal). Thus, $V_4 = V_2 - 3V = 8V - 3V = 5V$.
   • Node 1: A 6V voltage source is connected between Node 1 (negative terminal) and Node 3 (positive terminal). Thus, $V_1 = V_3 - 6V = 8V - 6V = 2V$.
   • Node 5: A 1V voltage source is connected between Node 7 (negative terminal) and Node 5 (positive terminal). Thus, $V_5 = V_7 + 1V = 8V + 1V = 9V$.

5. Summary of Node Potentials:

   • $V_1 = 2V$
   • $V_2 = 8V$
   • $V_3 = 8V$
   • $V_4 = 5V$
   • $V_5 = 9V$
   • $V_6 = 8V$
   • $V_7 = 8V$
   • $V_8 = 0V$
   • $V_9 = 8V$

The key is to use Nodal Analysis, choosing a reference node, and then using the voltage sources and direct wire connections to determine the potentials at all other nodes.