Question

calculate force on the vertex B andc

Answer 1

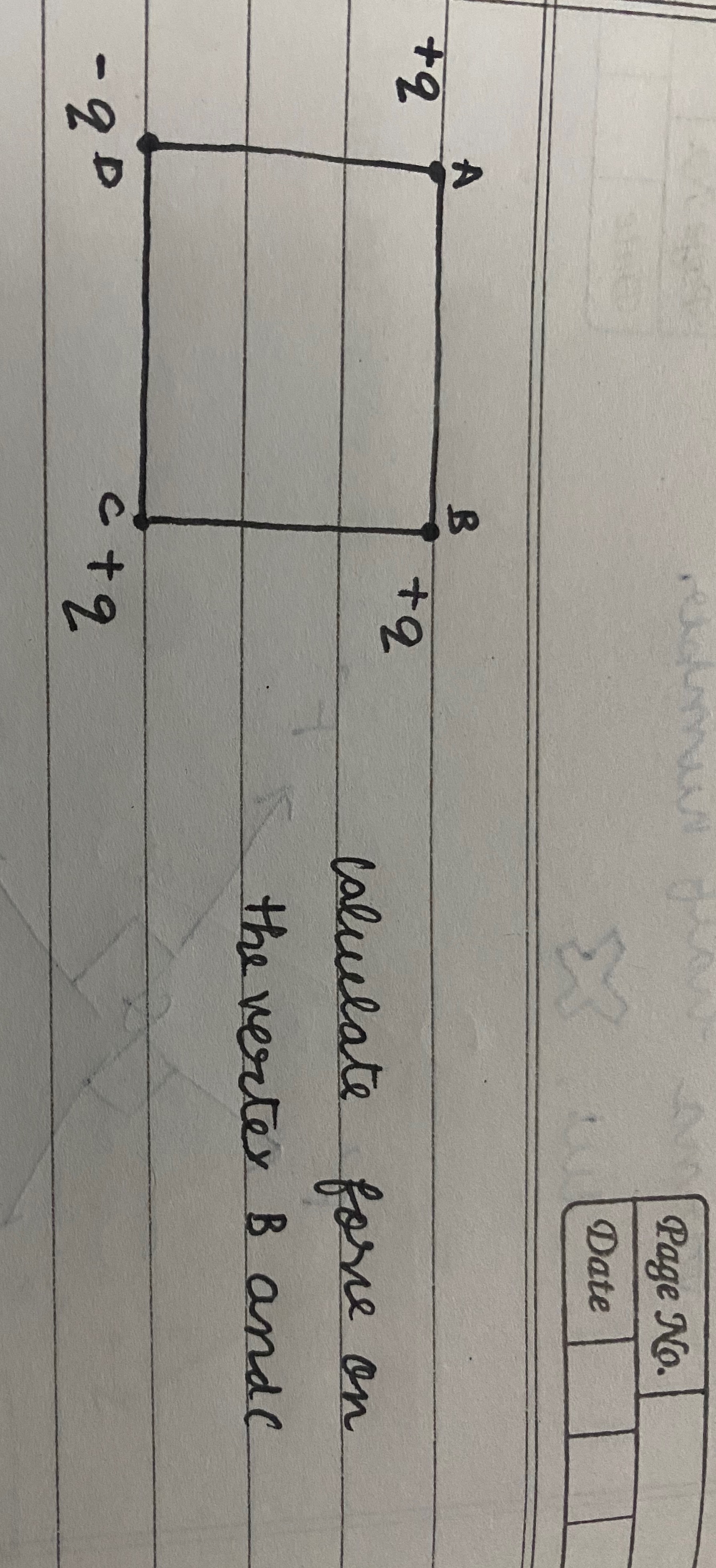
Force on vertex B:

$$\vec{F}_B = \frac{k}{a^2}\left[\left(4-\frac{2q}{\sqrt2}\right)\hat{i}+\left(\frac{2q}{\sqrt2}-2q\right)\hat{j}\right]$$

Force on vertex C:

$$\vec{F}_C = \frac{k}{a^2}\left[\left(\frac{q}{\sqrt2}-2q^2\right)\hat{i}+\left(\frac{q}{\sqrt2}+2q\right)\hat{j}\right]$$

Answer 2

We choose a square of side length a with vertices

A = (0, 0), B = (a, 0), C = (a, a) and D = (0, a).

The charges are

A: +2, B: +2, C: +q, D: –2q.

All forces are calculated by Coulomb’s law

F = k·(q₁q₂)/r²

and the direction (attraction or repulsion) is decided by the signs of the charges.

Step 1. Force on B

The net force on charge at B (q_B = +2) is the vector sum of the forces due to A, C and D.

1. Force due to A (charge +2 at (0,0)):

   • Separation: AB = a.
   • Magnitude: F_BA = k · (2×2)/a² = (4k)/a².
   • Direction: Since both charges are positive the force is repulsive; B is repelled away from A. The vector from A to B is (a, 0) so

   F_BA = (4k/a²) î.

2. Force due to C (charge +q at (a,a)):

   • Separation: BC = a.
   • Magnitude: F_BC = k · (2×q)/a² = (2kq)/a².
   • Since both are positive, the force is repulsive. The line joining B to C is vertical (from B = (a,0) to C = (a,a)); so B is repelled in the opposite direction of C, i.e. downward.

   F_BC = (2kq/a²)(–ĵ).

3. Force due to D (charge –2q at (0,a)):

   • Separation: Distance from B = (a,0) to D = (0,a) is r = √(a²+a²)= a√2.
   • Magnitude: F_BD = k · |2×(–2q)|/(a√2)² = k · (4q)/(2a²) = (2kq)/a².
   • B is positive and D is negative so the force is attractive. The vector from B to D is D – B = (0–a, a–0) = (–a, a). Its unit vector is

   u = (–a, a)/(a√2) = (–1/√2, 1/√2).

   Thus, F_BD = (2kq/a²)(–1/√2 î + 1/√2 ĵ).

Now summing all contributions (using î, ĵ for the unit vectors in x and y directions):

• x‐component:

  F_B,x = (4k/a²) + (–2kq/(a²√2))

• y‐component:

  F_B,y = (–2kq/a²) + (2kq/(a²√2))

Thus,

$$\vec{F}_B = \frac{k}{a^2}\left[\left(4-\frac{2q}{\sqrt2}\right)\hat{i}+\left(\frac{2q}{\sqrt2}-2q\right)\hat{j}\right]\,.$$

Step 2. Force on C

Now the charge at C is +q. Its force arises from charges at A (+2), B (+2) and D (–2q).

1. Force due to A (at (0,0)):

   • Separation: from A to C is along the diagonal: AC = a√2.
   • Magnitude: F_CA = k · (q×2)/(a√2)² = k·(2q)/(2a²)= kq/a².
   • Direction: Since both are positive, repulsion pushes C in the direction from A to C. The vector A→C = (a, a) with unit vector (1/√2, 1/√2).

   Thus, F_CA = (kq/a²)(1/√2 î + 1/√2 ĵ).

2. Force due to B (at (a,0)):

   • Separation: BC = a.
   • Magnitude: F_CB = k · (q×2)/a² = 2kq/a².
   • Both positive so the force on C is repulsive; the line from B to C is vertical upward.

   Thus, F_CB = (2kq/a²) ĵ.

3. Force due to D (at (0,a)):

   • Separation: CD = a (since C = (a,a), D = (0,a)).
   • Magnitude: F_CD = k · |q×(–2q)|/a² = (2kq^2)/a².
   • Since C is positive and D is negative, the force is attractive. The vector from C to D is (0–a, a–a) = (–a, 0) with unit vector (–1, 0).

   Thus, F_CD = –(2kq^2/a²) î.

Now summing for C:

• x‐component:

  F_C,x = (kq/(a²√2)) – (2kq^2/a²)

• y‐component:

  F_C,y = (kq/(a²√2)) + (2kq/a²)

Thus,

$$\vec{F}_C = \frac{k}{a^2}\left[\left(\frac{q}{\sqrt2}-2q^2\right)\hat{i}+\left(\frac{q}{\sqrt2}+2q\right)\hat{j}\right]\,.$$

Summary of the Answer

1. Force on vertex B:

$$\vec{F}_B = \frac{k}{a^2}\left[\left(4-\frac{2q}{\sqrt2}\right)\hat{i}+\left(\frac{2q}{\sqrt2}-2q\right)\hat{j}\right]$$

2. Force on vertex C:

$$\vec{F}_C = \frac{k}{a^2}\left[\left(\frac{q}{\sqrt2}-2q^2\right)\hat{i}+\left(\frac{q}{\sqrt2}+2q\right)\hat{j}\right]$$

Any answer that is algebraically equivalent is correct.