Question

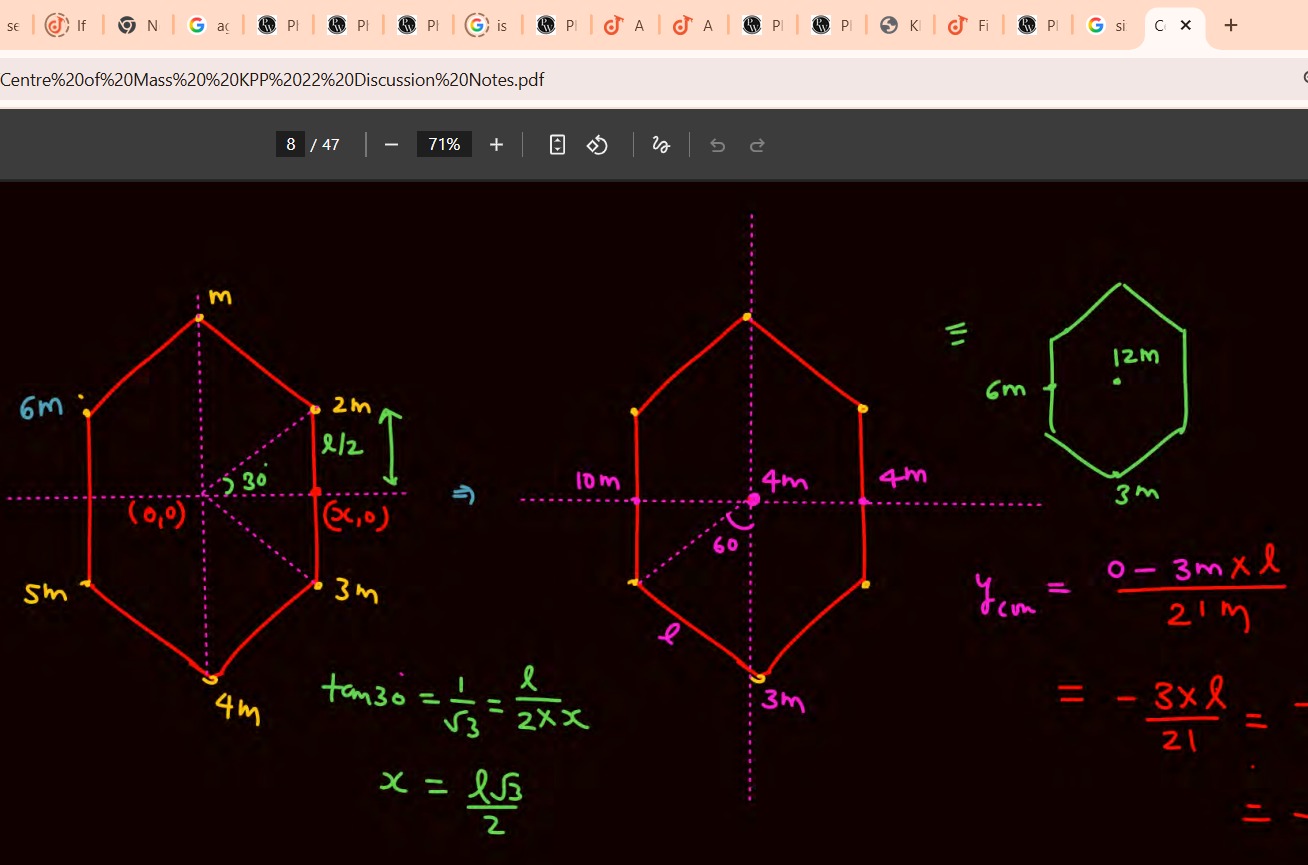
A system of masses is located at the vertices of a regular hexagon. The origin (0,0) is at the center of the hexagon. The dashed lines represent the x and y axes. The distances from the center to each vertex are equal to 'l'. The masses and their locations are as follows:

• Mass 'm' is at (0, l).
• Mass '2m' is at $(\frac{l\sqrt{3}}{2}, \frac{l}{2})$.
• Mass '3m' is at $(\frac{l\sqrt{3}}{2}, -\frac{l}{2})$.
• Mass '4m' is at (0, -l).
• Mass '5m' is at $(-\frac{l\sqrt{3}}{2}, -\frac{l}{2})$.
• Mass '6m' is at $(-\frac{l\sqrt{3}}{2}, \frac{l}{2})$.

Find the coordinates of the center of mass of this system.

Answer 1

The center of mass is at $\left(-\frac{l\sqrt{3}}{7}, -\frac{l}{7}\right)$.

Answer 2

The total mass is $M = m + 2m + 3m + 4m + 5m + 6m = 21m$.

The x-coordinate of the center of mass is: $X_{cm} = \frac{1}{M} \sum m_i x_i$ $X_{cm} = \frac{1}{21m} \left( m(0) + 2m(\frac{l\sqrt{3}}{2}) + 3m(\frac{l\sqrt{3}}{2}) + 4m(0) + 5m(-\frac{l\sqrt{3}}{2}) + 6m(-\frac{l\sqrt{3}}{2}) \right)$ $X_{cm} = \frac{1}{21m} \left( ml\sqrt{3} + \frac{3ml\sqrt{3}}{2} - \frac{5ml\sqrt{3}}{2} - 3ml\sqrt{3} \right)$ $X_{cm} = \frac{ml\sqrt{3}}{21m} \left( 1 + \frac{3}{2} - \frac{5}{2} - 3 \right) = \frac{l\sqrt{3}}{21} \left( \frac{2+3-5-6}{2} \right) = \frac{l\sqrt{3}}{21} \left( \frac{-6}{2} \right) = \frac{l\sqrt{3}}{21}(-3) = -\frac{l\sqrt{3}}{7}$

The y-coordinate of the center of mass is: $Y_{cm} = \frac{1}{M} \sum m_i y_i$ $Y_{cm} = \frac{1}{21m} \left( m(l) + 2m(\frac{l}{2}) + 3m(-\frac{l}{2}) + 4m(-l) + 5m(-\frac{l}{2}) + 6m(\frac{l}{2}) \right)$ $Y_{cm} = \frac{1}{21m} \left( ml + ml - \frac{3ml}{2} - 4ml - \frac{5ml}{2} + 3ml \right)$ $Y_{cm} = \frac{ml}{21m} \left( 1 + 1 - \frac{3}{2} - 4 - \frac{5}{2} + 3 \right) = \frac{l}{21} \left( 2 - \frac{3+5}{2} - 4 + 3 \right) = \frac{l}{21} \left( 2 - 4 - 4 + 3 \right) = \frac{l}{21} (-3) = -\frac{l}{7}$

Thus, the center of mass is at $\left(-\frac{l\sqrt{3}}{7}, -\frac{l}{7}\right)$.