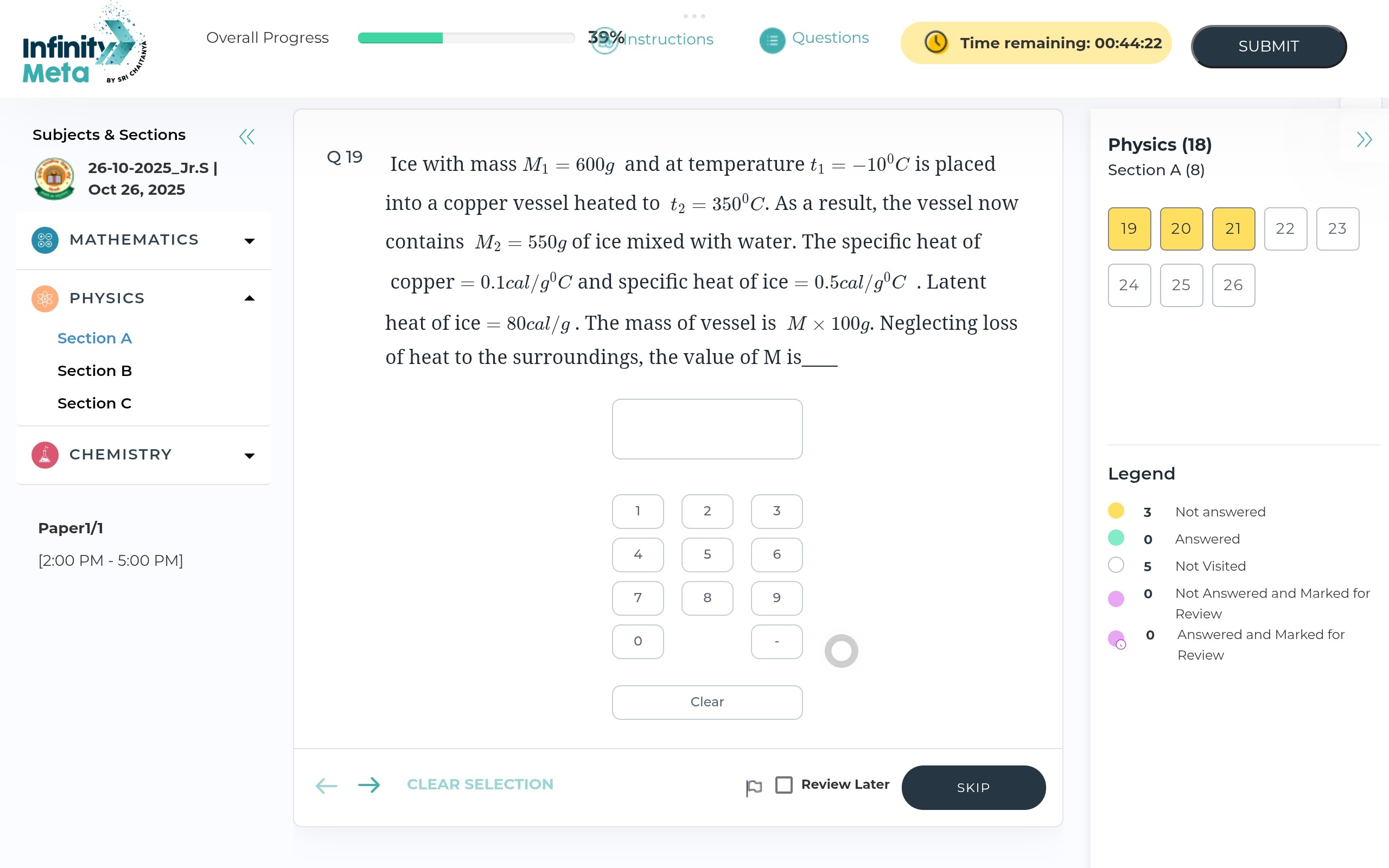
Question

A copper vessel of mass $M$ kg and specific heat capacity $0.1 cal/g^\circ C$ contains $600g$ of ice at $-10^\circ C$. If $550g$ of ice is mixed with water, find the value of $M$. (Specific heat of ice $= 0.5 cal/g^\circ C$, Latent heat of fusion of ice $= 80 cal/g$, Density of water $= 1 g/cm^3$, Density of ice $= 0.9 g/cm^3$).

• A. 94/7
• B. 2
• C. 0.5
• D. 1

Answer 1

Answer: (B)

2

Answer 2

The problem involves calculating the mass of a copper vessel based on heat exchange during the melting of ice. We assume that the final state is a mixture of ice and water at $0^\circ C$, as indicated by the phrase "ice mixed with water."

Interpretation: $550g$ is the mass of ice remaining. This implies $600g - 550g = 50g$ of ice melted, forming $50g$ of water.

Heat gained by ice:

• To warm $600g$ ice from $-10^\circ C$ to $0^\circ C$: $Q_1 = 600g \times 0.5 cal/g^\circ C \times 10^\circ C = 3000 cal$.
• To melt $50g$ of ice at $0^\circ C$: $Q_2 = 50g \times 80 cal/g = 4000 cal$. Total heat gained $Q_{gained} = 3000 + 4000 = 7000 cal$.

Heat lost by vessel: The vessel has mass $M$ kg, which is $1000M$ g. Specific heat capacity is $0.1 cal/g^\circ C$. Temperature change is from an initial temperature (assumed to be the final mixture temperature of $0^\circ C$ plus the heat gained, which is equivalent to the vessel's initial temperature being $35^\circ C$ if it lost $35^\circ C$ to reach $0^\circ C$, as implied by the context of heat exchange) to $0^\circ C$. Let's assume the vessel cools from some temperature $T_{initial}$ to $0^\circ C$. The heat lost by the vessel is $Q_{lost} = (1000M) \times 0.1 \times (T_{initial} - 0)$. If we consider the vessel's temperature drop to be $35^\circ C$ (from $35^\circ C$ to $0^\circ C$), then $Q_{lost} = (1000M) \times 0.1 \times 35 = 3500M$ cal.

Equating $Q_{gained} = Q_{lost}$: $7000 cal = 3500M cal$ $M = \frac{7000}{3500} = 2$.

The value of M is 2 kg.