Question

$10\sqrt{3}m/s$

Answer 1

30 m/s

Answer 2

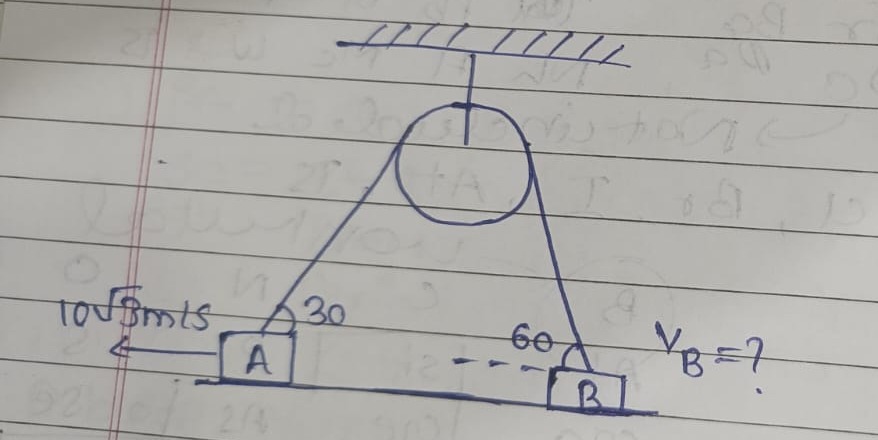
The problem involves a fixed pulley and an inextensible string connecting two blocks, A and B. The blocks are moving horizontally. We need to find the velocity of block B ($V_B$) given the velocity of block A ($V_A$) and the angles the string segments make with the horizontal.

1. Identify the Constraint:

The key constraint in this system is that the length of the string is constant. For an inextensible string passing over a fixed pulley, the speed of the string must be the same on both sides of the pulley. This means the component of the velocity of each block along the string must be equal in magnitude.

2. Component of Velocity along the String:

• For Block A:

  Block A moves horizontally with a velocity $V_A = 10\sqrt{3}$ m/s. The string segment connected to block A makes an angle of $30^\circ$ with the horizontal. The component of $V_A$ along the string is $V_A \cos(30^\circ)$. This represents the rate at which the string is being pulled by block A.

• For Block B:

  Let the velocity of block B be $V_B$. Assuming block B moves horizontally to the right (which is expected if A moves left and pulls the string). The string segment connected to block B makes an angle of $60^\circ$ with the horizontal. The component of $V_B$ along the string is $V_B \cos(60^\circ)$. This represents the rate at which the string is being pulled by block B.

3. Apply the Constraint Equation:

Since the string is inextensible and the pulley is fixed, the rates at which the string is pulled on both sides must be equal in magnitude:

$V_A \cos(30^\circ) = V_B \cos(60^\circ)$

4. Substitute Values and Solve:

Given:

$V_A = 10\sqrt{3}$ m/s

$\cos(30^\circ) = \frac{\sqrt{3}}{2}$

$\cos(60^\circ) = \frac{1}{2}$

Substitute these values into the equation:

$(10\sqrt{3}) \times \left(\frac{\sqrt{3}}{2}\right) = V_B \times \left(\frac{1}{2}\right)$

Simplify the equation:

$10 \times \frac{3}{2} = V_B \times \frac{1}{2}$

$15 = \frac{V_B}{2}$

Solve for $V_B$:

$V_B = 15 \times 2$

$V_B = 30$ m/s

The velocity of block B is $30$ m/s.