Question

10cm

-20cm

10cm

d

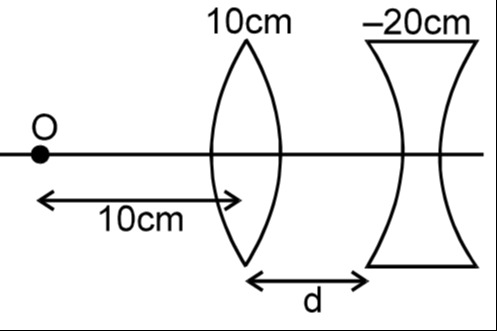
• A. 10cm
• B. -20cm
• C. 10cm
• D. d

Answer 1

Answer: (A)

d = 10 cm

Answer 2

Solution:

1. For the converging lens:

   • Object distance, $u_1 = 10$ cm, and focal length, $f_1 = 10$ cm.
   • Using the lens formula: $$\frac{1}{f_1} = \frac{1}{v_1} + \frac{1}{u_1}\quad\Longrightarrow\quad \frac{1}{10} = \frac{1}{v_1} + \frac{1}{10}$$ This gives $\frac{1}{v_1} = 0$ so $v_1 = \infty$ (rays emerging are parallel).

2. For the diverging lens:

   • Its focal length is $f_2 = -20$ cm.
   • Parallel rays (from infinity) incident on a lens give an image distance $v_2 = f_2$, so here $v_2 = -20$ cm (image appears 20 cm in front of the diverging lens).
   • Let the separation between the lenses be $d$ (with the diverging lens at $x = d$) and place the converging lens at $x=0$. The object $O$ is at $x = -10$ cm.
   • The image formed by the diverging lens will be at $$x = d + v_2 = d - 20.$$
   • For the final image to coincide with the original object at $x = -10$: $$d - 20 = -10 \quad\Longrightarrow\quad d = 10\text{ cm}.$$

Explanation of the Minimal Core Solution:

1. For the converging lens: $u_1 = 10$ cm, $f_1 = 10$ cm gives $v_1 = \infty$ (parallel rays).
2. For the diverging lens: parallel rays yield $v_2 = -20$ cm.
3. Final image position $= d - 20$ must equal the object position $-10$ cm, so $d = 10$ cm.