Question

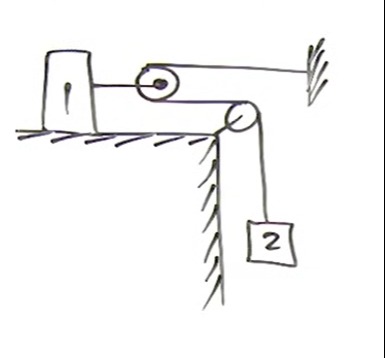
A block of mass $m_1$ is placed on a frictionless horizontal surface. A string is attached to the block, passes over two fixed pulleys, and is then attached to a hanging mass of $m_2$. Determine the acceleration of the system.

• A. The acceleration cannot be determined without knowing the masses $m_1$ and $m_2$.
• B. The acceleration is $a = \frac{m_1g}{m_1 + m_2}$.
• C. The acceleration is $a = \frac{m_2g}{m_1 + m_2}$.
• D. The acceleration is $a = \frac{m_1g}{m_2}$.

Answer 1

Answer: (C)

The acceleration is $a = \frac{m_2g}{m_1 + m_2}$.

Answer 2

The system consists of a block of mass $m_1$ on a frictionless horizontal surface and a hanging mass of $m_2$, connected by a string passing over two fixed pulleys. Let $T$ be the tension in the string and $a$ be the magnitude of the acceleration of the system.

Applying Newton's second law to the block of mass $m_1$ on the horizontal surface: The only horizontal force is the tension $T$ pulling it to the right. $\Sigma F_x = m_1a$ $T = m_1a$ (Equation 1)

Applying Newton's second law to the hanging mass $m_2$: The forces acting on $m_2$ are its weight $m_2g$ downwards and the tension $T$ upwards. Since the mass is accelerating downwards, the net force is $m_2g - T$. $\Sigma F_y = m_2a$ $m_2g - T = m_2a$ (Equation 2)

Now, substitute the expression for $T$ from Equation 1 into Equation 2: $m_2g - (m_1a) = m_2a$

Rearrange the terms to solve for $a$: $m_2g = m_1a + m_2a$ $m_2g = (m_1 + m_2)a$

Therefore, the acceleration of the system is: $a = \frac{m_2g}{m_1 + m_2}$