Question

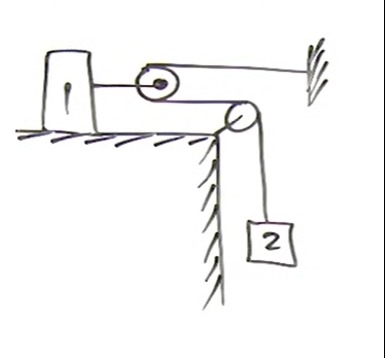
The provided question is missing. Based on the explanation, it appears to involve a system with blocks and pulleys, likely asking for the relationship between the accelerations of block '1' and weight '2'.

• A. The acceleration of block '1' is equal to the acceleration of weight '2'.
• B. The acceleration of block '1' is twice the acceleration of weight '2'.
• C. The acceleration of block '1' is half the acceleration of weight '2'.
• D. The acceleration of block '1' is opposite to the acceleration of weight '2'.

Answer 1

Answer: (A)

The acceleration of block '1' is equal to the acceleration of weight '2'.

Answer 2

Let $x_1$ be the position of block '1' to the right, and $y_2$ be the vertical position of weight '2' downwards. Let $x_{p1}$ be the horizontal position of the movable pulley P1 to the right. The string is attached to block '1', goes around the movable pulley P1, then around the fixed pulley P2, and finally to weight '2'. The length of the string segments are: from block '1' to P1 is $x_{p1} - x_1$, from P1 to P2 is $X_{P2} - x_{p1}$, and from P2 to weight '2' is $y_2$. The total length of the string $L$ is constant: $L = (x_{p1} - x_1) + (X_{P2} - x_{p1}) + y_2 = X_{P2} - x_1 + y_2$. Differentiating with respect to time, we get the relationship between velocities: $0 = -\frac{dx_1}{dt} + \frac{dy_2}{dt}$, which means $v_1 = v_2$. Differentiating again with respect to time, we get the relationship between accelerations: $a_1 = a_2$. Therefore, the acceleration of block '1' is equal to the acceleration of weight '2'.