Question

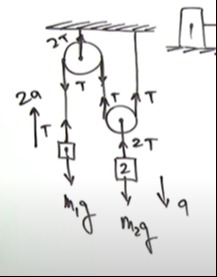
A pulley system consists of two masses, $m_1$ and $m_2$. The mass $m_1$ moves upwards with an acceleration of $2a$, and mass $m_2$ moves downwards with an acceleration of $a$. Let $T$ be the tension in the string. Determine the accelerations of $m_1$ and $m_2$ and the tension $T$ in terms of $m_1$, $m_2$, and $g$.

• A. The acceleration of $m_1$ upwards is $a_1 = 2g \frac{m_2 - 2m_1}{m_2 + 4m_1}$, and the acceleration of $m_2$ downwards is $a_2 = g \frac{m_2 - 2m_1}{m_2 + 4m_1}$.
• B. The acceleration of $m_1$ upwards is $a_1 = g \frac{m_2 - 2m_1}{m_2 + 4m_1}$, and the acceleration of $m_2$ downwards is $a_2 = 2g \frac{m_2 - 2m_1}{m_2 + 4m_1}$.
• C. The acceleration of $m_1$ upwards is $a_1 = 2g \frac{2m_1 - m_2}{m_2 + 4m_1}$, and the acceleration of $m_2$ downwards is $a_2 = g \frac{2m_1 - m_2}{m_2 + 4m_1}$.
• D. The acceleration of $m_1$ upwards is $a_1 = g \frac{2m_1 - m_2}{m_2 + 4m_1}$, and the acceleration of $m_2$ downwards is $a_2 = 2g \frac{2m_1 - m_2}{m_2 + 4m_1}$.

Answer 1

Answer: (A)

The acceleration of $m_1$ upwards is $a_1 = 2g \frac{m_2 - 2m_1}{m_2 + 4m_1}$, and the acceleration of $m_2$ downwards is $a_2 = g \frac{m_2 - 2m_1}{m_2 + 4m_1}$.

Answer 2

To solve this problem, we apply Newton's Second Law to each mass.

Let $a$ be the magnitude of the downward acceleration of mass $m_2$. The problem states that the upward acceleration of mass $m_1$ is $2a$. Let $T$ be the tension in the string.

For mass $m_1$: The forces acting on $m_1$ are tension $T$ upwards and gravitational force $m_1g$ downwards. Applying Newton's second law (taking the upward direction as positive): $T - m_1g = m_1(2a)$ (Equation 1)

For mass $m_2$: The forces acting on $m_2$ are the upward pull from two string segments, each with tension $T$ (total upward force $2T$), and gravitational force $m_2g$ downwards. Applying Newton's second law (taking the downward direction as positive for $m_2$): $m_2g - 2T = m_2a$ (Equation 2)

Solving the system of equations: From Equation 1, we can express the tension $T$: $T = m_1g + 2m_1a$

Substitute this expression for $T$ into Equation 2: $m_2g - 2(m_1g + 2m_1a) = m_2a$ $m_2g - 2m_1g - 4m_1a = m_2a$

Rearrange the terms to solve for $a$: $m_2g - 2m_1g = m_2a + 4m_1a$ $g(m_2 - 2m_1) = a(m_2 + 4m_1)$ $a = g \frac{m_2 - 2m_1}{m_2 + 4m_1}$

This value of $a$ is the downward acceleration of mass $m_2$. The acceleration of mass $m_1$ upwards is $2a$: $2a = 2g \frac{m_2 - 2m_1}{m_2 + 4m_1}$

Therefore, the acceleration of block $m_1$ upwards is $a_1 = 2g \frac{m_2 - 2m_1}{m_2 + 4m_1}$, and the acceleration of block $m_2$ downwards is $a_2 = g \frac{m_2 - 2m_1}{m_2 + 4m_1}$.