Question

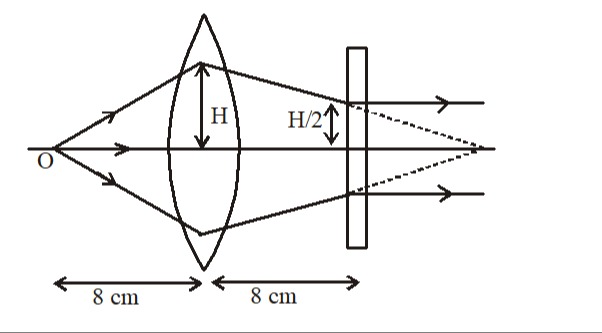
Ray diagram showing the path of light rays through a converging lens and a rectangular block. A point source 'O' emits light rays that pass through a converging lens. The distance from the point source 'O' to the lens is labeled as 8 cm. The height of the light rays at the lens is labeled as 'H'. After passing through the lens, the light rays converge and then pass through a rectangular block. The distance from the lens to the rectangular block is labeled as 8 cm. The height of the light rays at the rectangular block is labeled as 'H/2'. After passing through the rectangular block, the light rays travel parallel to the central axis. Dashed lines indicate the path of the light rays if the rectangular block were not present.

Answer 1

The focal length of the converging lens is $\frac{16}{3}$ cm.

Answer 2

Solution:

1. Finding the image position (v):

   • Without the block, a ray from the top of the object meets the lens at height $H$ and then goes to the image point. Linear variation (by similar triangles) gives the height at a distance $x$ from the lens as $$\text{Height} = H\left(1-\frac{x}{v}\right)$$
   • At $x=8$ cm (where the block is located), if no block were present, the height would be $$H\left(1-\frac{8}{v}\right)$$
   • But the block forces the ray height to be $\frac{H}{2}$. Equate: $$H\left(1-\frac{8}{v}\right)=\frac{H}{2}$$ Cancel $H$ (assuming $H\ne0$): $$1-\frac{8}{v}=\frac{1}{2} \quad\Longrightarrow\quad \frac{8}{v}=\frac{1}{2} \quad\Longrightarrow\quad v=16\text{ cm}$$

2. Using the Lens Formula:
   The lens formula is

   $$\frac{1}{f}=\frac{1}{u}+\frac{1}{v}$$

   Given $u=8$ cm and $v=16$ cm, we have

   $$\frac{1}{f}=\frac{1}{8}+\frac{1}{16}=\frac{2}{16}+\frac{1}{16}=\frac{3}{16}$$

   Thus,

   $$f=\frac{16}{3}\text{ cm}\approx5.33\text{ cm}$$

Core Explanation:

• Use similar triangles to equate the expected height at 8 cm to $\frac{H}{2}$.
• Solve $1-\frac{8}{v}=\frac{1}{2}$ to get $v=16$ cm.
• Apply lens formula: $\frac{1}{f}=\frac{1}{8}+\frac{1}{16}=\frac{3}{16}$ so $f=\frac{16}{3}$ cm.