Question
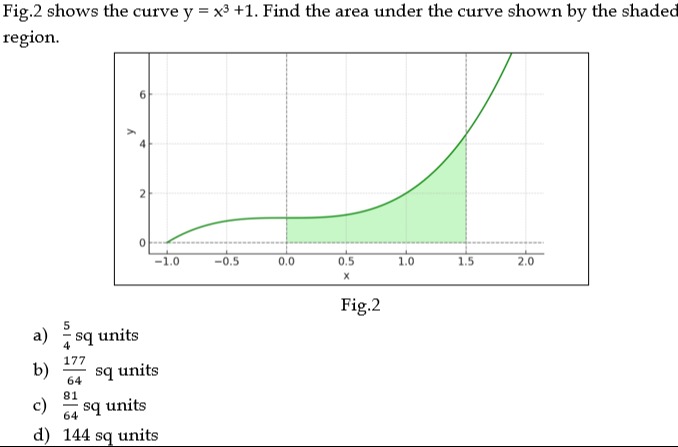
Question: Fig.2 shows the curve y = x³ +1. Find the area under the curve shown by the shaded region....
Fig.2 shows the curve y = x³ +1. Find the area under the curve shown by the shaded region.
45 sq units
64177 sq units
6481 sq units
144 sq units
64177 sq units
Solution
The shaded region represents the area under the curve y=x3+1 from x=0 to x=1.5. To find this area, we need to evaluate the definite integral of the function y=x3+1 with respect to x from the lower limit 0 to the upper limit 1.5.
The area A is given by:
A=∫01.5(x3+1)dx
First, find the indefinite integral:
∫(x3+1)dx=3+1x3+1+x+C=4x4+x+C
Now, evaluate the definite integral using the limits:
A=[4x4+x]01.5
Substitute the upper limit (x=1.5) and the lower limit (x=0):
A=(4(1.5)4+1.5)−(4(0)4+0)
A=4(1.5)4+1.5
Converting 1.5 to a fraction: 1.5=23.
A=4(23)4+23=42434+23=41681+23=16×481+23=6481+23
To add the fractions, find a common denominator, which is 64:
23=2×323×32=6496
A=6481+6496=6481+96=64177
Therefore, the area under the curve is 64177 square units.
