Question

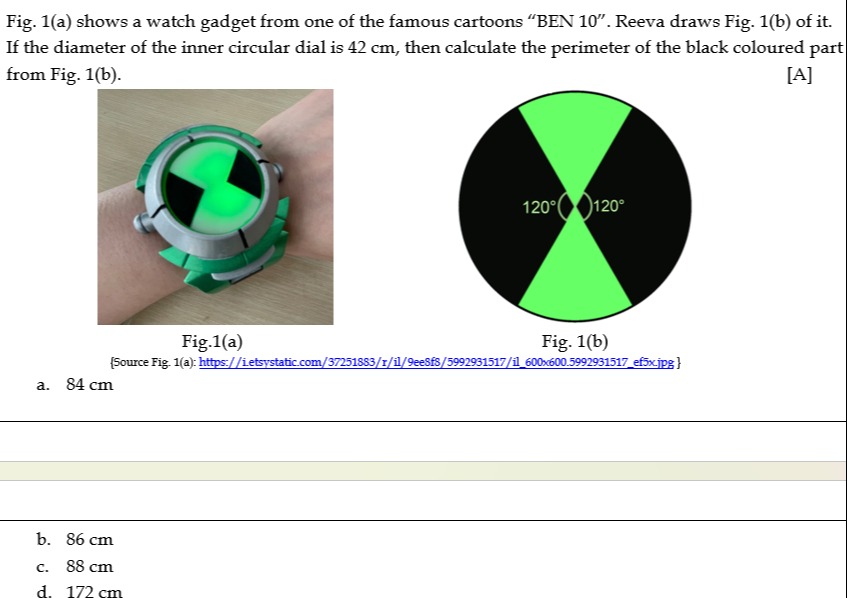
Fig. 1(a) shows a watch gadget from one of the famous cartoons "BEN 10". Reeva draws Fig. 1(b) of it. If the diameter of the inner circular dial is 42 cm, then calculate the perimeter of the black coloured part from Fig. 1(b). [A]

• A. 84 cm
• B. 86 cm
• C. 88 cm
• D. 172 cm

Answer 1

Answer: (A)

84 cm

Answer 2

To calculate the perimeter of the black coloured part, we first need to understand the geometry of the figure and the meaning of "perimeter" in this context.

1. Identify the given information:

   • The diameter of the inner circular dial is 42 cm.
   • The figure (Fig. 1(b)) shows a circle divided into four sectors: two green and two black.
   • The angles of the two green sectors are 120° each.

2. Calculate the radius:

   • Radius (R) = Diameter / 2 = 42 cm / 2 = 21 cm.

3. Determine the angles of the black sectors:

   • The sum of angles in a circle is 360°.
   • Total angle of the green sectors = 120° + 120° = 240°.
   • Total angle of the black sectors = 360° - 240° = 120°.
   • Since there are two black sectors, and they appear symmetrical, the angle of each black sector (let's call it $\theta$) = 120° / 2 = 60°.

4. Interpret "perimeter of the black coloured part": The black coloured part consists of two separate sectors. The perimeter of a single sector is typically defined as the sum of its arc length and the lengths of its two radii.

   • Arc length (L) of one sector = $\frac{\theta}{360^\circ} \times 2\pi R$
   • Perimeter of one sector = L + 2R

   Let's calculate the arc length of one black sector: $L = \frac{60^\circ}{360^\circ} \times 2 \times \frac{22}{7} \times 21$ $L = \frac{1}{6} \times 2 \times 22 \times 3$ $L = \frac{1}{6} \times 132$ $L = 22$ cm

   Perimeter of one black sector = $22 \text{ cm} + 2 \times 21 \text{ cm} = 22 + 42 = 64$ cm. If the question asks for the total perimeter of the black coloured part (meaning the sum of the perimeters of the two disjoint black sectors), then it would be $2 \times 64 \text{ cm} = 128$ cm.

   However, 128 cm is not among the given options. Let's re-examine the options and a possible alternative interpretation of the question.

   • a. 84 cm
   • b. 86 cm
   • c. 88 cm
   • d. 172 cm

   The option 84 cm is exactly $4 \times R$. This corresponds to the sum of the lengths of the four straight lines (radii) that form the boundaries of the two black sectors. Each black sector has two radii as its straight edges. Since there are two black sectors, there are $2 \times 2 = 4$ such radii in total. Sum of lengths of straight edges = $4 \times R = 4 \times 21 \text{ cm} = 84$ cm.

   While "perimeter" usually includes all boundary components (both curved and straight), in some competitive exam questions, if the options don't match the standard interpretation, an alternative interpretation focusing on a specific part of the boundary (like only straight lines or only arcs) might be intended. Given that 84 cm is an option and corresponds to the total length of the straight edges of the black parts, this is the most likely intended answer. The option 88 cm is the sum of the arc lengths of the green sectors ($2 \times 44 \text{ cm} = 88 \text{ cm}$). This is also not what is asked.

   Therefore, assuming the question implies only the straight boundaries of the black coloured parts:

   Total length of the straight boundaries of the black coloured part = (Number of black sectors) $\times$ (Number of radii per sector) $\times$ (Length of one radius) $= 2 \times 2 \times R$ $= 4 \times 21 \text{ cm}$ $= 84$ cm