Question
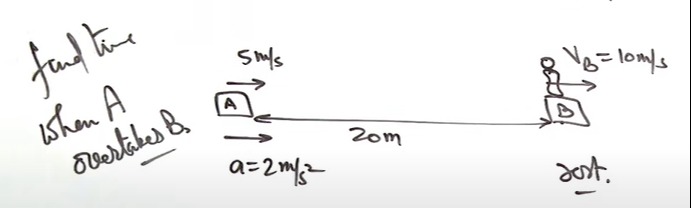
Question: When A overtakes B....
When A overtakes B.
The time when A overtakes B is 25+105 seconds.
The time when A overtakes B is 25−105 seconds.
The time when A overtakes B is 5 seconds.
The time when A overtakes B is 10 seconds.
The time when A overtakes B is 25+105 seconds.
Solution
Let xA(t) and xB(t) be the positions of objects A and B at time t. We set the initial position of object A as the origin, so xA0=0. Given:
- Initial velocity of A: vA0=5m/s
- Acceleration of A: aA=2m/s2
- Initial position of B: xB0=20m
- Velocity of B: vB=10m/s (constant)
The position of object A at time t is given by: xA(t)=xA0+vA0t+21aAt2 xA(t)=0+5t+21(2)t2 xA(t)=5t+t2
The position of object B at time t is given by: xB(t)=xB0+vBt xB(t)=20+10t
Object A overtakes object B when their positions are equal, i.e., xA(t)=xB(t). 5t+t2=20+10t
Rearranging the terms to form a quadratic equation: t2−5t−20=0
Using the quadratic formula t=2a−b±b2−4ac: t=2(1)5±(−5)2−4(1)(−20) t=25±25+80 t=25±105
Since time must be positive, we take the positive root: t=25+105 seconds.
