Question

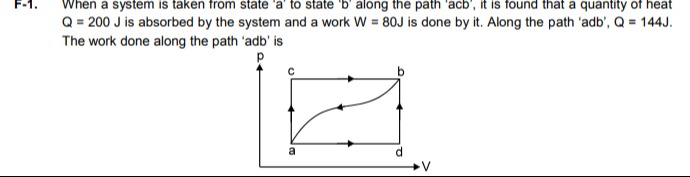
When a system is taken from state 'a' to state 'b' along the path 'acb', it is found that a quantity of heat Q = 200 J is absorbed by the system and a work W = 80J is done by it. Along the path 'adb', Q = 144J. The work done along the path 'adb' is

Answer 1

24 J

Answer 2

The first law of thermodynamics states that the change in internal energy $\Delta U$ of a system is given by $\Delta U = Q - W$, where $Q$ is the heat added to the system and $W$ is the work done by the system.

Internal energy is a state function, meaning that the change in internal energy between two states depends only on the initial and final states, not on the path taken.

For the path 'acb', the system goes from state 'a' to state 'b'. Given heat absorbed, $Q_{acb} = 200 \, \text{J}$. Given work done by the system, $W_{acb} = 80 \, \text{J}$. The change in internal energy from 'a' to 'b' along path 'acb' is: $\Delta U_{ab} = Q_{acb} - W_{acb} = 200 \, \text{J} - 80 \, \text{J} = 120 \, \text{J}$.

For the path 'adb', the system also goes from state 'a' to state 'b'. Given heat absorbed, $Q_{adb} = 144 \, \text{J}$. Let the work done by the system along path 'adb' be $W_{adb}$. The change in internal energy from 'a' to 'b' along path 'adb' is: $\Delta U_{ab} = Q_{adb} - W_{adb} = 144 \, \text{J} - W_{adb}$.

Since the change in internal energy between states 'a' and 'b' is independent of the path, the change in internal energy along path 'acb' is equal to the change in internal energy along path 'adb'. $\Delta U_{ab} (\text{along acb}) = \Delta U_{ab} (\text{along adb})$ $120 \, \text{J} = 144 \, \text{J} - W_{adb}$

Solving for $W_{adb}$: $W_{adb} = 144 \, \text{J} - 120 \, \text{J}$ $W_{adb} = 24 \, \text{J}$.

The work done along the path 'adb' is 24 J.