Question

Express the trigonometric ratios $\sin A,\sec A,\tan A$ in terms of $\cot A$. Write all the other trigonometric ratios of $\angle A$ in terms of $\sec A$.

Answer 1

We try to form the ratios in the form of sides of a right-angle triangle. Then we try to form the expressions of the $\sin A,\sec A,\tan A$ in terms of $\cot A$. We use different interconnecting trigonometric identities to find relations.

Complete step-by-step solution

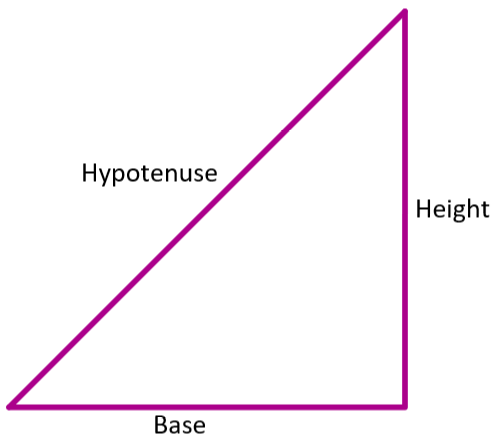
We need to express trigonometric ratios $\sin A,\sec A,\tan A$ in terms of $\cot A$.
We try to express the ratios in the form of sides of a right-angle triangle. We have three sides of the triangle as height/normal, base, and hypotenuse. The hypotenuse is the longest side of the triangle.
We know that $\cot A=\dfrac{base}{height}$. We also have $\sin A=\dfrac{height}{hypotenuse}$, $\sec A=\dfrac{hypotenuse}{base}$, $\tan A=\dfrac{height}{base}$.
Now $\sin A=\dfrac{1}{\cos ecA}$. We can express $\operatorname{cosec}A$ as a function of $\cot A$ where $\operatorname{cose}cA=\sqrt{1+{{\cot }^{2}}A}$.
So, $\sin A=\dfrac{1}{\cos ecA}=\dfrac{1}{\sqrt{1+{{\cot }^{2}}A}}$.
For the second case $\sec A=\sqrt{1+{{\tan }^{2}}A}$. We can express $\tan A$ as a function of $\cot A$ where $\tan A=\dfrac{1}{\cot A}$.
So, $\sec A=\sqrt{1+{{\tan }^{2}}A}=\sqrt{1+{{\left( \dfrac{1}{\cot A} \right)}^{2}}}=\dfrac{\sqrt{{{\cot }^{2}}A+1}}{\cot A}$.
For the final one $\tan A=\dfrac{1}{\cot A}$.
The remaining trigonometric ratios are $\cos A$ and $\cos ecA$. We need to express them in terms of $\sec A$.
We have $\cos A=\dfrac{base}{hypotenuse}$ and $\cos ecA=\dfrac{hypotenuse}{height}$.
So, $\cos A=\dfrac{1}{\sec A}$ for the first relation.
For the second case $\cos ecA=\dfrac{1}{\sin A}$. We can express $\sin A$ as a function of $\cos A$ where $\sin A=\sqrt{1-{{\cos }^{2}}A}$. We also have $\cos A=\dfrac{1}{\sec A}$. So, $\sin A=\sqrt{1-{{\cos }^{2}}A}=\sqrt{1-\dfrac{1}{{{\sec }^{2}}A}}$.
Replacing values, we get $\cos ecA=\dfrac{1}{\sqrt{1-\dfrac{1}{{{\sec }^{2}}A}}}=\dfrac{\sec A}{\sqrt{{{\sec }^{2}}A-1}}$.

Note: All the trigonometric ratios are related to each other. We also could have used a variable to find the values of the ratios. We take the variable as $\cot A=x$. We find the relations and put the variable in place of $\cot A$.