Question

Express tan A in terms of sin A.

Answer 1

Hint: To solve this problem, we will write tan A in terms of sin A and cos A (that is $\tan A=\dfrac{\sin A}{\cos A}$). We will then square both the sides. We can then express ${{\cos }^{2}}A=1-{{\sin }^{2}}A$ to get ${{\tan }^{2}}A$ in terms of ${{\sin }^{2}}A$. We can then get the value of tan A by performing the square root on both sides of the equation.

Complete step-by-step solution -

We first try to understand the trigonometric properties in terms of a right triangle ABC (as shown below).

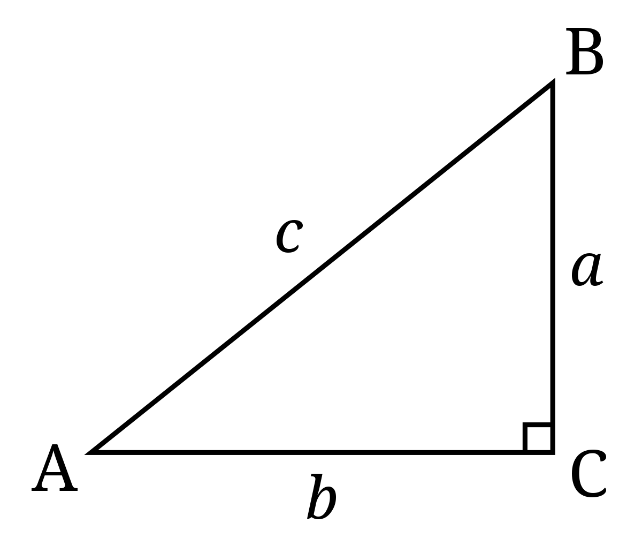
Now, by definition, we have,
sin A = $\dfrac{a}{c}$ -- (1)
cos A = $\dfrac{b}{c}$ -- (2)
tan A = $\dfrac{a}{b}$
Thus, we can see that $\dfrac{\sin A}{\cos A}=\tan A$ . Now, to proceed forward, we square both LHS and RHS, thus, we get,
${{\left( \dfrac{\sin A}{\cos A} \right)}^{2}}={{\tan }^{2}}A$
$\left( \dfrac{{{\sin }^{2}}A}{{{\cos }^{2}}A} \right)={{\tan }^{2}}A$ -- (A)
Now, we square (1) and (2) individually and then adding them, we get,
${{\sin }^{2}}A+{{\cos }^{2}}A=\dfrac{{{a}^{2}}+{{b}^{2}}}{{{c}^{2}}}$ -- (3)
Now, we can use the Pythagoras theorem on the right triangle. We have,
${{a}^{2}}+{{b}^{2}}={{c}^{2}}$
We put this in (3), we get,
$\begin{aligned} & {{\sin }^{2}}A+{{\cos }^{2}}A=\dfrac{{{c}^{2}}}{{{c}^{2}}} \\\ & {{\sin }^{2}}A+{{\cos }^{2}}A=1 \\\ \end{aligned}$
Now, we can substitute the value of ${{\cos }^{2}}A=1-{{\sin }^{2}}A$ in (A), we get,
$\left( \dfrac{{{\sin }^{2}}A}{1-{{\sin }^{2}}A} \right)={{\tan }^{2}}A$
Now, simplifying further, we get,
To find tan A in terms of sin A, we just perform square root on both RHS and LHS, we get.
$\tan A=\sqrt{\dfrac{{{\sin }^{2}}A}{1-{{\sin }^{2}}A}}$
$\tan A=\dfrac{\sin A}{\sqrt{1-{{\sin }^{2}}A}}$ -- (B)
Thus, equation (B) gives us the relation between tan A and sin A.

Note: It is generally important to remember few results like ${{\cos }^{2}}A=1-{{\sin }^{2}}A$ , since this result greatly helps us in arriving at the results faster. Generally, for finding any trigonometric angle in terms of other trigonometric angles (say cot A in terms of cos A), we have to square both the terms to use the known results and then we can perform square root to get the desired relation.